A Guide to Writing in Mathematics Classes

Table of Contents

I. Why Should You Have To Write Papers In A Math Class ?
II. How is Mathematical Writing Different?
III. Following the Checklist
IV. Good Phrases to Use in Math Papers
V. Helpful Hints for the Computer
VI. Other Sources of Help

I. Why Should You Have To Write Papers In A Math Class?

For most of your life so far, the only kind of writing you've done in math classes has been
on homework and tests, and for most of your life you've explained your work to people
that know more mathematics than you do (that is, to your teachers). But soon, this will
change.

With each additional mathematics course you take, you further distance yourself from the
average person on the street. You may feel like the mathematics you can do is simple and
obvious (doesn't everybody know what a function is?), but you can be sure that other
people find it bewilderingly complex . It becomes increasingly important, therefore, that
you can explain what you're doing to others that might be interested: your parents, your
boss, the media.

Nor are mathematics and writing far- removed from one another . Professional
mathematicians spend most of their time writing: communicating with colleagues,
applying for grants, publishing papers, writing memos and syllabi. Writing well is
extremely important to mathematicians, since poor writers have a hard time getting
published, getting attention from the Deans, and obtaining funding. It is ironic but true
that most mathematicians spend more time writing than they spend doing math.
But most of all, one of the simplest reasons for writing in a math class is that writing
helps you to learn mathematics better. By explaining a difficult concept to other people,
you end up explaining it to yourself.

Every year, we buy ten cases of paper at $35 each; and every year we sell them for about
$1 million each. Writing well is very important to us.

- Bill Browning, President of Applied Mathematics, Inc.

II. How is Mathematical Writing Different from What You 've Done So Far?

A good mathematical essay has a fairly standard format. We tend to start solving a
problem by first explaining what the problem is, often trying to convince others that it's
an interesting or worthwhile problem to solve. On your homework, you've usually just
said, "9(a)" and then plunged ahead; but in your formal writing, you'll have to take much
greater pains.

After stating what the problem is, we usually then state the answer, even before we show
how we got it. Sometimes we even state the answer right along with the problem. It's
uncommon, although not so uncommon as to be exceptional, to read a math paper in
which the answer is left for the very end. Explaining the solution and then the answer is
usually reserved for cases where the solution technique is even more interesting than the
answer, or when the writers want to leave the readers in suspense. But if the solution is
messy or boring, then it's typically best to hook the readers with the answer before they
get bogged down in details.

Another difference is that when you do your homework, it is important to show exactly
how you got your answer. However, when you write to a non-mathematician, sometimes
it's better to show why your answer works, with just a brief explanation as to how you got
it. For example, compare :

Homework Mathematics:

To solve for x when 3x² − 21x + 30 = 0 , we use the quadratic formula:

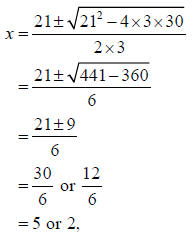
and so either x = 5 or x = 2 .

More Formal Mathematics:
To solve for x when 3x² − 21x + 30 = 0 , we used the quadratic formula and
found that either x = 5 or x = 2 . It's easy to see that these are the right answers,
because

3×5² − 21×5 + 30 = 0

and also

3×2² − 21× 2 + 30 = 0

The difference is that, in the first example, you're trying to convince someone who knows
a lot of math that you know what you're doing (and if you don't, to get partial credit). In
the second example, you're trying to show someone who may or may not be good at math
that you got the right answer.

Math is difficult enough that the writing around it should be simple. ‘Beautiful’ math
papers are the ones that are the easiest to read: clear explanations, uncluttered expositions
on the page, well-organized presentation. For that reason, mathematical writing is not a
creative endeavor the same way that, say, poetry is: you shouldn't be spending a lot of
time looking for the perfect word , but rather should be developing the clearest exposition.
Unlike humanities students, mathematicians don't have to worry about over-using ‘trite’
phrases in mathematics. In fact, at the end of this booklet is a list of trite but useful
phrases that you may want to use in your papers, either in this class or in the future

This guide, together with your checklist, should serve as a reference while you write. If
you can master these basic areas, your writing may not be spectacular, but it should be
clear and easy to read - which is the goal of mathematical writing, after all.

III. Following the checklist

When you turn in your writing assignment, you should attach the checklist to the front.
You should feel free to use both the checklist and this booklet as a guide while you write,
because you will be graded directly on the criteria outlined on the checklist. What follows
here is a more detailed explanation of the criteria I use for grading your papers.

1. Clearly restate the problem to be solved.

Do not assume that the reader knows what you're talking about. (The person you're
writing to might be out on vacation, for example, or have a weak memory). You don't
have to restate every detail, but you should explain enough so that someone who's never
seen the assignment can read your paper and understand what's going on, without any
further explanation from you. Outline the problem carefully.

2. State the answer in a complete sentence which stands on its own.

If you can avoid variables in your answer, do so; otherwise, remind the reader what they
stand for. If your answer is at the end of the paper and you've made any significant
assumptions, restate them, too. Do not assume that the reader has actually read every
word and remembers it all (do you?).

3. Clearly state the assumptions which underlie the formulas .

For example, what physical assumptions do you have to make? (No friction, no air
resistance? That something is lying on its side, or far away from everything else?)
Sometimes things are so straightforward that there are no assumptions, but not often.

4. Provide a paragraph which explains how the problem will be approached.

It's not polite to plunge into mathematics without first warning your reader. Carefully
outline the steps you're going to take, giving some explanation of why you're taking that
approach. It's nice to refer back to this paragraph once you're deep in the thick of your
calculations .

5. Clearly label diagrams, tables, graphs, or other visual representations of the math
(if these are indeed used).

In math, even more than in literature, a picture is worth a thousand words, especially if
it's well labeled. Label all axes, with words, if you use a graph. Give diagrams a title
describing what they represent. It should be clear from the picture what any variables in
the diagram should represent. The whole idea is to make everything as clear and self-explanatory
as possible.

If you decide to draw pictures in you will (a) have a lot of fun, and (b) waste a lot of time.
If you're going to draw diagrams on the computer, I recommend doing so in the early
stages of the project, and then saving the document so you can change it later -because
you'll have to change it later, and you can't do it once it's in Word or whatever.

6. Define all variables used.

(a) Even if you label your diagram (and you should), you should still explain in words
what your variables are.
(b) If there's a quantity you use only a few times, see if you can get away with not
assigning it a variable. As examples:

Figure 1: Diagram of the triangle (Each square is 1" x 1")	We see that the area of the triangle will be one-half of the product of its height and base - that is, the area of the triangle is (1/2) x 3 x 4 = 6 square inches.
	We see that A = (1/2)bh, where A stands for the area of the triangle, b stands for the base of the triangle, and h stands for the height of the triangle, and so A = (1/2) x 4 x 3 = 6 square inches.

Elementary physics tells us that the velocity of a falling body is proportional to the amount of time it has already spent falling. Therefore, the longer it falls, the faster it goes.
Elementary physics tells us that v(t ) = g (t − t0 ), where v(t ) is the velocity of the falling object at time t,g is gravity, and  t0 is the time at which the object is released. Therefore as t increases, so does v(t ): i.e., as time increases, so does velocity.

I hope that you'll agree that the first example of each pair is much easier to read.

(c) The more specific you are, the better. State the units of measurement. When you can
use words like "of", "from", "above", etc., do so. For example:

We get the equation d =rt, where d is the distance, r is the rate, and t is the time.
We get the equation d = rt , where d is the distance from Sam's car to her home (in miles), r is the speed at which she's traveling (measured in miles per hour), and t is the number of hours she's been on the road.

Avoid words like "position" (height above ground? sitting down? political situation?) and
"time" (5 o'clock? January? 3 minutes since the experiment started?). Never mind that
your instructor uses these words freely; you can too when you get a Ph.D.