College Algebra

ANGEL is the general CFCC course management system. The login protocol is
<student id number> for the ID with Password <lastname> until you change the
password. For any technical problems with ANGEL

Tentative Schedule

Due to unforeseen events, it may be necessary for the course schedule to be
altered. The instructor will always strive to be fair about any changes.

Course Description: This course is a study of functions. The course covers
linear, absolute value, exponential, logarithmic, quadratic, and rational and
radical functions and their applications. The course presents these concepts
through an applied approach. Other topics include systems of equations,
composition of functions and inverse functions. This course is intended for those
students who need additional preparation before precalculus mathematics as
well as those whose major programs specifically require this level of
mathematics.

Administrative dates:
Add/Drop Aug 19 – 21, Drop only Aug 24 – 25, Last day for refund Aug 25, Next
semester schedule posted on the web Oct 12, Last day to drop with “W” Oct 29
Labor Day Sep 7, No day classes Oct 6, Thanksgiving Nov 26 – 27.

Math Center Hours: M – Th 8am – 6pm; F 8am – 3pm

Attendance is mandatory, though nonattendance does not constitute withdrawal
from this course – it is the student’s responsibility to complete the withdrawal

College Preparatory Courses–State law requires no more than three attempts
TOTAL to complete all college preparatory (mathematics and reading) courses.
Students registered in college prep courses who receive N grade must repeat the
same course and complete it with a grade of C of better before they can register
for other courses.

Topics by Section in Rockswold:

Ch.Sec	Topics
1.2	Distance; Midpoint
1.3	Representations of Functions; Formal Definition; Identifying Functions
1.4	Constant, Linear, Non- Linear Functions ; Slope; Average Rate of Change; Difference Quotient
2.1	Representations of Linear Functions
2.2	Forms for Equations of Lines ; Intercepts; Horizontal, Vertical, Parallel and Perpendicular Lines
2.3	Equations; Symbolic Solutions
2.4	Inequalities; Interval Notation; Compound Inequalities
2.5	Evaluating and Graphing Piecewise Linear Functions; Absolute Value Function; Equations and Inequalities with Absolute Value
3.1	Vertex Formula; Applications
3.2	Quadratic Equations
3.3	Quadratic Inequalities
3.4	Vertical and Horizontal Translations; Stretching and Shrinking; Reflections; Combining Transformations given Functions in Standard Form
4.1	Identifying Polynomials; A Function’s Intervals of Increase and Decrease, Concavity and Extrema; Symmetry
4.2	Graphs of Polynomials (End-Behavior, Degree and y-Intercept)
4.3	Division by Monomials ; The Factor Theorem; Graphs and Multiple Zeros
4.4	Complex Numbers; Quadratic and Polynomial Equations with Complex Solutions
4.5	Vertical and Horizontal Asymptotes
4.6	Polynomial and Rational Inequalities
4.7	Radical Equations
5.1	Composition
5.2	One-to-One Functions; Finding Formula for an Inverse Function
5.3	Linear vs. Exponential Growth; Compound Interest; Natural Exponential
5.4	Common Log; Basic Equations;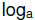
5.5	Properties of Logarithms
5.6	Exponential and Logarithmic Equations
6.1	Linear and Non-Linear Systems of Equations; Joint Variation
6.2	Systems of Linear Inequalities

Course Objectives
1. The student will use new vocabulary that is introduced and taught directly;
2. The student will write in a variety of informational/expository forms, including
a variety of technical documents (e.g., howtomanuals, procedures, assembly
directions);
3. The student will identify the real and imaginary parts of complex numbers and
perform basic operations.
4. The student will graph absolute value equations and inequalities in two
variables.
5. The student will identify and graph common functions (including but not
limited to linear, rational, quadratic, cubic , radical, absolute value).
6. The student will perform operations (addition, subtraction, division and
multiplication) of functions algebraically , numerically, and graphically.
7. The student will determine the composition of functions.
8. The student will describe and graph transformations of functions
9. The student will solve problems involving functions and their inverses.
10. The student will solve problems using direct, inverse, and joint variations.
11. The student will solve literal equations for a specified variable.
12. The student will solve and graph the solutions of absolute value equations
and inequalities with one variable.
13. The student will write an equation of a line given any of the following
information: two points on the line, its slope and one point on the line, or its
graph. Also, The student will find an equation of a new line parallel to a given
line, or perpendicular to a given line, through a given point on the new line.
14. The student will solve systems of linear equations and inequalities in two and
three variables using graphical , substitution, and elimination methods .
15. The student will solve realworld problems involving systems of linear
equations and inequalities in two and three variables.
16. The student will factor polynomial expressions.
17. The student will divide polynomials by monomials and polynomials with
various techniques, including synthetic division.
18. The student will graph polynomial functions with and without technology and
describe end behavior.
19. The student will use theorems of polynomial behavior (including but not
limited to the Fundamental Theorem of Algebra, Remainder Theorem, the
Rational Root Theorem, Descartes' Rule of Signs , and the Conjugate Root
Theorem) to find the zeros of a polynomial function.
20. The student will write a polynomial equation for a given set of real and/or
complex roots.
21. The student will describe the relationships among the solutions of an
equation, the zeros of a function, the xintercepts of a graph, and the factors of a
polynomial expression, with and without technology.
22. The student will use graphing technology to find approximate solutions for
polynomial equations.
23. The student will use polynomial equations to solve realworld problems.
24. The student will add, subtract, multiply, and divide rational expressions.
25. The student will simplify complex fractions .
26. The student will solve rational equations.
27. The student will add, subtract, multiply and divide radical expressions (square
roots and higher).
28. The student will simplify expressions using properties of rational exponents.
29. The student will convert between rational exponent and radical forms of
expressions.
30. The student will solve equations that contain radical expressions.
31. The student will solve quadratic equations over the real numbers by
completing the square.
32. The student will use the discriminant to determine the nature of the roots of a
quadratic equation.
33. The student will solve quadratic equations over the complex number system.
34. The student will identify the axis of symmetry, vertex, domain, range and
intercept (s) for a given parabola.
35. The student will define exponential and logarithmic functions and determine
their relationship
36. The student will define and use the properties of logarithms to simplify
logarithmic expressions and to find their approximate values.
37. The student will graph exponential and logarithmic functions.
38. The student will solve logarithmic and exponential equations.
39. The student will use the change of base formula.
40. The student will solve applications of exponential growth and decay.
41. The student will decide whether a given statement is always, sometimes, or
never true (statements involving linear or quadratic expressions, equations, or
inequalities rational or radical expressions or logarithmic or exponential
functions).
42. The student will define arithmetic and geometric sequences and series.
43. The student will find specified terms of arithmetic and geometric sequences.