Developing Double-Digit Division Skills in Children

Learning Problem:

“Julia loves using math workbooks . We buy them at local bookstores whenever she gets the urge. She
studies math in spurts, yet moves fairly quickly through the books when inspired. When she came upon
long division, however, she asked for my help. I explained the mechanics and what it meant in real terms,
but she was stumped.“

“When teaching long division, students often forget what to do next after they bring down a number.”

“We are doing some hard math--DIVISION! Single- digit division isn't too bad, but the double-digit
examples are a little bit harder. Please help by making sure your child knows the multiplication facts
instantly.“

As suggested by the large number of web pages addressing the issue, double-digit division is a
troublesome learning concept for many students. It appears that even students demonstrating an interest
or ability in math may have trouble with double-digit division. The number of steps involved in solving one
problem often throws students for a loop when they first encounter these types of problems in 4th or 5th
grade. Halfway through the problem, the student may even forget what to do next. As the last quote
suggests, the biggest issue with learning double-digit division may be the fact that students have not
mastered the necessary component skills. This problem becomes even more readily apparent when
students are asked to solve word problems with double-digit division. Without the foundation and
prerequisite skills , students cannot be expected to solve problems in a complex situation.

Needs Assessment:

In order to gain a better understanding of the problem of teaching and learning double-digit division, a
study must be conducted in which the present learning environment is analyzed. In turn, this may provide
us with insight into how double-digit division could be better taught. Therefore, we must complete a
thorough needs assessment that examines the current practices in the classroom and evaluates their
effectiveness. Based on our hypothesis that the behavioral perspective on learning would best teach
them the necessary skills for double-digit division, we intend to model our needs assessment on the
design principles that reinforce this type of learning.

Design Principle	Rationale for Principle	Study	How to Test
Information and Procedures are presented systematically (taking into account what students already know)	In order for students to learn about a difficult concept, they must first understand the individual components of the concept, subtraction, multiplication, simple division, word problem analysis and organization skills.	Prior Knowledge: We need to determine what skills the students already have in place in terms of basic mathematics. Can they subtract? Can they solve simple word problems? Components: An analysis of the components of double-digit division must be undertaken in order to create a learnable sequence. Here, we must identify all of the necessary components skills and rules for teaching double-digit division.	We will conduct a pre-test of math skills for all students, in order to identify their strengths and weaknesses. We will also complete a literature review, to determine the complete and most effective sequence for teaching double-digit division.
Controlled Practice with Feedback	Behaviorism supports the learning of knowledge through controlled practice with feedback. We need to know if this is already present in the learning environment and if not, what practices are already in place. This will give us a guideline for what is working and what is not.	Present Methods: The current methods of teaching double-digit division in the classroom need to be analyzed. Are teachers using repetition with students? Are they teaching under controlled circumstances? Do students know when they are right, and when they’ve made a mistake?	We will observe the current math classroom and interview teachers to find out their methods and rationale. What do they think is working – what are the current deficiencies?
Promotion of Errorless Learning	In addition, behaviorism supports learning environments where errors are not made. The environment we design should identify errors immediately and not allow students to continue until they have identified and corrected their mistakes.	Present Methods: Are students presently learning in an environment that allows them to create links between the stimulus and the wrong response? Are they allowed to make mistakes and continue on with their work? How much flexibility is built into their learning environment?	During our classroom observations, we will note whether students are making errors, particularly consistent ones. How much feedback is available in the classroom now to identify and remedy students’ errors?
Practice should occur in simple contexts	Practice of stimulus-response situations should not complicate learning in any way. How are students being asked to learn double-digit division now? Are they using complicated word problems or intricate games? If so, this environment may be too complicated to build the links desired.	Present Methods: We must examine the context in which double-digit division is being taught. Are teachers using the simplest methods, or are they cluttering practice by introducing more difficult or irrelevant concepts.	We will interview students and teachers here, asking them to describe how they practice this skill. Perhaps the students will view their work differently than their teachers who assigned it. This method will give us both perspectives.
Sequence of Component-to- Composite Skills	Learning is most effective when it teaches simple skills, creates links between them that constitute rules, and then builds on those rules to create coherent knowledge.	Present Methods: The order of presentation of double-digit division components in the current learning environment should be studied. Are teachers incorrectly introducing the concept of division before securing the component concepts of subtraction and multiplication ? Are they testing to ensure that students have mastered basic concepts?	We need to work with teachers and observe classes in order to outline the steps that are currently used for teaching double-digit division in the classroom. Are they consistent between classes? Are they slowly progressive? Is there testing before moving to new skills?
Individualization	In behavioral learning, teaching is most effective when it is individualized for the strengths and deficiencies of each learner. Assumptions about where students should be learning are dangerous to the development of rule learning.	Present Methods: We must examine whether students are being taught according to their individual abilities. Are there tutors (such as computers) that can tailor skill building to the particular learner? Do the teachers have the time and inclination to focus on individual students, or are they taught as a class or in clusters?	We will take an inventory of the resources available to teachers. Are there enough teachers and aides in the school to individualize learning? Are there enough computers and corresponding software to address specific needs? Interviews with teachers can also help determine whether this is a possibility in the current structure of the school. Interviews with students will elicit their feelings on how their individual needs are being addressed.
Effective Use of Reinforcement	In order to incorporate effective use of reinforcement, the students’ motivations must be understood. Therefore, we can ensure that reinforcement is productive and appropriate to the individual.	Reinforcement: We must gather input from parents on the likes and desires of the children. In that way, reinforcements that are offered can then be individualized and serve as true motivation for students. Present Method: We must also determine whether reinforcement, particularly appropriate reinforcement at appropriate times, is now being used in the classroom.	Interviews with parents and students will determine a small number of reinforcements that can be offered for successes in learning. As part of our classroom observation, we will learn how reinforcement tools are now being used in the classroom. Are students adequately motivated? Are they reinforced after appropriate learning achievements?

With this important background knowledge, we can now begin to design a new learning environment that
uses behaviorist principles to improve the teaching of double-digit division. We will use the literature
review to plan our new design, and the observation, testing and interview results to understand how the
present teaching methods can inform our design suggestions. Perhaps most importantly, we will
understand what concepts are already in place, creating a jumping off point from which we can begin to
build new skills.

Planned Design:

The learning environment for acquiring the skills necessary for performing double-digit, long division word
problems could possibly be improved in our design by the learning activities defined in the following chart .
We have investigated the sequence of learning components as they pertain to the composite skill of
double-digit, long division problems. In conjunction, a learning procedure is suggested and defined. In
the end, chaining each of the learned concepts, procedures and rules should lead to a full understanding
of not only how to execute these complex division problems, but a foundational perception of the true
components of division problems.

It is important to note that arrangement and sequence of learning tasks must be based upon the
complexity of each component. The design will begin by enforcing mastery of small units of mathematics
(subtraction and multiplication); mastery of each subsequent unit must be completed before moving into
more complex units and chaining the procedures. The learning environment will begin with paper-based
drills and practice and then transition into individualized computer-learning programs, designed to better
shape students’ knowledge based on their personal progress and understanding.

Sequence of Component to Composite Skill	Concept	Recommended Procedure
Concept Learning of Information and Procedures	Pre-test students’ knowledge of basic underlying skills in math including subtraction and multiplication. Evaluate the outcome to determine if foundational concepts must be reviewed or re-learned. Develop concepts (basic skills) to mastery.	Using a paper-based, pre-test format, children will execute basic drills for math problems including subtraction and multiplication and basic division skills. The students will be required to work through multiple drills until mastery of these basic mathematics components. Teachers will evaluate their progress based on educational standards to be sure that students are ready to progress to the next sequence.
Rule Learning	Practice of repetitive drill problems using the following “DMS 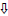” technique for each problem: D M S	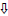In working the division problems, students will check each sequence in their progression against this chart. First the student needs to divide (D) and once the student writes quotient, draw a check mark beside the "D". Then (M) which tells the student that the next step is to multiply and check off the "M". Subtraction (S) is the next step in the division process and they will check off that they have subtracted. Finally, the down arrow ( 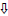) indicates bringing down the next number from the dividend. The student continues following the D, M, S, 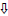.process by checking off components in each sequence of division problem.
Rule Learning (errorless learning in individualized, simple context environments)	Once the former skill is mastered, the child moves to a computer-aided environment to learn double-digit, long division rules in a self-paced, errorless learning environment. Errors in division may negatively influence progress since each calculation in the problem requires distinct accuracy of the former calculation.	In using computer-aided learning environment the ‘smart agent’ monitors student skill levels so they can work at all different levels (i.e.: children who have mastered the double-digit division concept and others who are learning at slower rates). Word problems are presented on the computer screen. Children work on ‘ graph paper ’ on the computer and the system will know whether the student entered the right number in the right space. The computer system catches students’ errors before they can be performed and alerts them to the mistakes that would occur if that answer had been entered incorrectly. Errors are noted and explained before they are made. If there is a mistake, the system requires the student to correct before they can proceed to the next step in the problem.
Problem Solving	Problem solving is the final stage in our division learning design. Once all sequences are fully developed by the student, they engage in longer problem solving tasks that continue to provide drills to practice long division skills.	Students would begin working on long word problems involving complex, long division drills. They should ultimately have gained the chaining knowledge to connect what parts of the word problem will require their long division skills and be able to transfer the knowledge and understanding of long division into more complex situations. Instead of simple, repetitive drill and practice problems, these word problems will involve additional information and students will have to properly filter the components they need to successfully perform the word problem.
Reinforcement	Reinforcement is a critical factor throughout each sequence of the learning design.	Children should be awarded points based on the amount of time they spend on problems or how many they get right. Rewards can also be delivered to children for the number of correct answers they’ve achieved on homework, quizzes and tests. The programmed reinforcements will be defined by teachers (individualized so that each students’ reward matches a behavioral response to accomplish the tasks). Depending on points, the teacher will decide how to award each child. Again, each stage in the sequence should involve reinforcement techniques. In order to encourage the children at each step, they will have to be rewarded appropriately.

Assessment:

In order to determine how effective our new learning environment is for teaching double-digit division
problem-solving skills, we will conduct pre- and post-test on basic skills and a composite understanding.
We would use simple, paper-based testing that requires students to write out their work clearly, step-by-step.
The pre-test, conducted before we institute our new design, would test subtraction, multiplication,
simple division and problem-solving skills.

Then we will initiate our new behavioral learning environment, teaching skills, creating links that make
rules and building them into more complicated processes. Afterward, we will conduct a paper-based
posttest with similar questions to the pre-test, with basic skills and more complicated questions. Is it clear
from their work that they now have mastered the components of the larger problems? Are they working
through the proper steps to reach their conclusion? What are they still missing?

The final part of our assessment will look at the reinforcements that have been integrated into learning.
Are they working as motivation for students? Are they appropriate to the individuals? Do we need to
change them to make them more effective?