Equations and Inequalities
Definition
Radical Equations are equations in which the variable is inside a radical.
Examples:
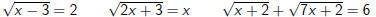
A radical equation may be transformed into a simple linear
or quadratic
equations. Sometimes the transformation process yields extraneous
solutions. These are apparent solutions that may solve the transformed
problem but are not solutions of the original radical equation.
Example (1)
Solve the equation 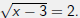
Transform the radical equation into a linear equation ...
The solution set is {7}.
Example (2)
Solve the equation 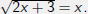
Transform the radical equation into a quadratic equation ...
The solution set is {3}.
Example (3)
Solve the equation 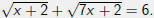
The solution set is {2}.
PROCEDURE FOR SOLVING RADICAL EQUATIONS
Step 1: Isolate the term with a radical on one side.
Step 2: Raise both (entire) sides of the equation to the power that
will eliminate this radical , and simplify the equation.
Step 3: If a radical remains, repeat steps 1 and 2.
Step 4: Solve the resulting linear or quadratic equation.
Step 5: Check the solutions and eliminate any extraneous solutions.
Equations that are higher order or that have fractional
powers often can
be transformed into a quadratic equation by introducing a u- substitution .
We say that equations are quadratic in form.
| ORIGINAL EQUATION | SUBSTITUTION | NEW EQUATION |
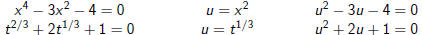 |
||
PROCEDURE FOR SOLVING EQUATIONS QUADRATIC IN
FORM
Step 1: Identify the substitution.
Step 2: Transform the equation into a quadratic form.
Step 3: Solve the quadratic equation.
Step 4: Apply the substitution to rewrite the solution in terms of
the original variable .
Step 5: Solve the resulting equation.
Step 6: Check the solutions in the original solutions.
Example (4)
Find the solution to the equation 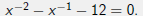
The solution set is 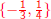 .
.
Example (5)
Find the solution to the equation 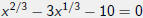 .
.
The solution set is {-8, 125}.
Some equations (both polynomial and with rational
exponents ) that are
factorable can be solved using the zero product property .
Example (6)
Solve the equation 
The solution set is {-1, 0,4}.
Example (7)
Solve the equation 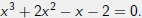
The solution set is {-2, -1, 1}.
| Prev | Next |