Foundations of Computational Math

Due date: 5PM Wednesday, 11/26/08
Grading: Since this overlaps with the assignment of Program 3, all of these questions
will be graded based on effort.

Problem 8.1

Suppose 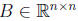is a symmetric positive definite tridiagonal matrix of the form

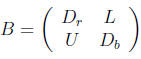
where n = 2k, D_r and D_b are diagonal matrices of order n/2, L is a lower triangular matrix
with nonzeros restricted to its main diagonal and its first subdiagonal, and U is upper
triangular matrix with nonzeros restricted to its main diagonal and its first superdiagonal.

Assume that Ax = b can be solved using Jacobi ’s method, i.e., the iteration converges
acceptably fast. Partition each iterate x_i into the top half and bottom half, i.e.,

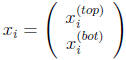
8.1.a. Assume an initial guess x₀ is given and identify what information, i.e., the pieces
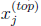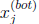of x_i for 0≤i≤j, determines the values found in the vectors and for any j > 0.

8.1.b. Can the relationships from 8.1.a be used to design an iteration that approximates
the solution essentially as well but only requires half of the work of Jacobi’s
method ?

8.1.c. Relate your new method from 8.1.b to applying Gauss-Seidel to solve Bx = b
starting from the same initial guess x₀.

Problem 8.2

8.2.a

Consider the two matrices :

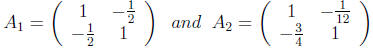
Suppose you solve systems of linear equations involving A₁ and A₂ using Jacobi’s method.
For which matrix would you expect faster convergence?

8.2.b

Consider the matrix

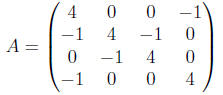
(i) Will Jacobi’s method converge when solving Ax = b?
(ii) Will Gauss-Seidel converge when solving Ax = b?

Problem 8.3

Consider solving a linear system Ax = b where A is symmetric positive definite using steepest descent.

(8.3.a) Suppose you use steepest descent without preconditioning . Show that the residuals,
r_k and r_k+1 are orthogonal for all k.

(8.3.b) Suppose you use steepest descent with preconditioning . Are the residuals, r_k
and r_k+1 are orthogonal for all k? If not is there any vector from step k that is
guaranteed to be orthogonal to r_k+1?

Problem 8.4

Let f(x) = x^3 − 3x + 1. This polynomial has three distinct roots

(8.4.a) Consider using the iteration function

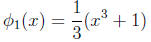
Which, if any, of the three roots can you compute with 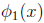and how would you
choose x⁽⁰⁾ for each computable root?

(8.4.b) Consider using the iteration function

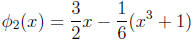
Which, if any, of the three roots can you compute with 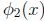and how would you
choose x⁽⁰⁾ for each computable root?

(8.4.c) For each of the roots you identified as computable using eithe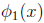r or ,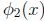
apply the iteration to find the values of the roots . (You need not turn in any
code, but using a simple program to do this is recommended.)

8.4.d

Let 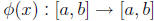be a continuous function. Show that if 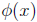is a contraction mapping
on [a, b] then the sequence {x^(k)} defined by x^(k+1) = 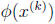is a Cauchy sequence.