Fractions
Section 3: Equivalent Fractions
Definition: When two fractions represent the same
amount with respect to the same "whole", the two fractions
are said to be equivalent.
Example 1:
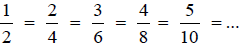
All of these fractions are equivalent because they
represent the same value on the number line .
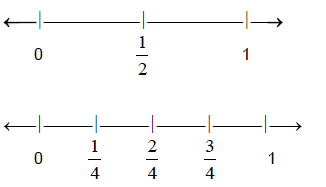
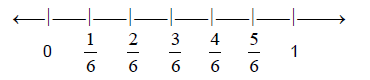
If a, b, and c are integers and b and c are not 0, then it is always true that
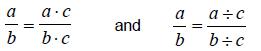
in other words, if the numerator and the denominator of a
fraction are multiplied or divided
by the same nonzero number, the resulting fraction is equivalent to the original
fraction.
Example 2:
Write 2/5 as an equivalent fraction with a denominator of 25.
Solution : The denominator of the original fraction
is 5. The fraction we are trying to find must have
a denominator of 25. We know that if we multiply 5 by 5, we get 25. The property
above
indicates that we can multiply the denominator by 5 as long as we do the same to
the
numerator.
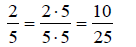
The fraction 2/5 is equivalent to 10/25.
Example 3:
Write 12/18 as an equivalent fraction with a denominator of 6.
Solution: If we divide the original denominator 18
by 3, we get 6. The property above
indicates that if we divide both the numerator and denominator by 3, we will get
an
equivalent fraction.
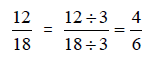
The fraction 12/18 is equivalent to 4/6.
**********************************************************************************************************************************
**
Now You Try (Section 3.1)
1) Write 7/8 as an equivalent fraction with a denominator
of 48.
2) Write 24/40 as an equivalent fraction with a denominator of 5.
(Answers to Now You Try (Section 3.1) are found on page
29.)
Two fractions a/b and c/d are equivalent if ad = bc. In other words, 2 fractions
are equal when their cross
products are equal.
Example 1: Are
Are 4/5 and 11/15 equivalent?
Solution: Two fractions are equal if their cross products are equal. Since 4 * 15 ≠ 5 * 11,4/5 and 11/15 are not equivalent.
**********************************************************************************************************************************
**
Now You Try (Section 3.2)
Determine if the following pairs of fractions are equivalent.
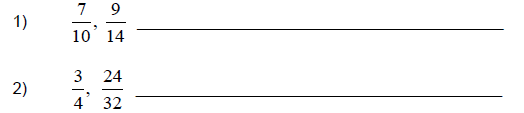
(Answers to Now You Try (Section 3.2) are found on page
29.)
**********************************************************************************************************************************
**
Section 4: Comparing Fractions
Now that we can determine if two fractions are equivalent,
the next topic is to determine which is greater.
Models are useful in determining which fraction is larger, so before we find a
general formula , try the following
examples:
Example 1:
Shade the regions that correspond to the fractions 2/3 and 7/12 on the rectangles below.
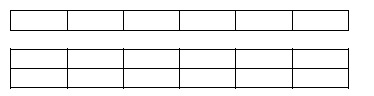
Which fraction is larger? __________
Solution:
1) Shade 2/3 by dividing the region up into 3 sections (4
rectangles in each section),
then shade 2 of the sections.
| xxxx | xxxx | xxxx | xxxx | ||
| xxxx | xxxx | xxxx | xxxx |
2) Shade 7/12 by shading in 7 of the 12 equal parts
| xxxx | xxxx | xxxx | xxxx | ||
| xxxx | xxxx | xxxx |
Therefore, 2/3 is larger since there are 8 of the 12 equal parts shaded.
Example 2:
Use the sets below to determine which is the larger fraction:
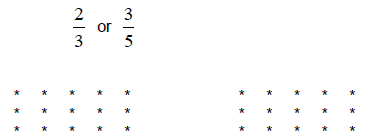
Solution: 1) Circle 2/3 of the stars in the 1st grouping.
10 stars circled
2) Circle 3/5 of the stars in the 2nd grouping .
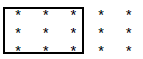
9 stars circled
Therefore, 2/3 is larger since there were 10 stars circled.
Notice that in the 2 model examples, the visual
representations were actually showing the common denominators
for the fractions. In example 1, there were 12 equal parts and 12 is the common
denominator between 3 and 12.
In example 2, there were 15 stars and 15 is the common denominator between 3 and
5.
General Rule for Determining Which Fraction is Greater
Case 1: Fractions with common denominators
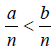if and only if a < b.
In other words, if the denominators are the same, compare the numerators.
Case 2: Fractions with like denominators .
Now consider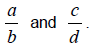 
We know
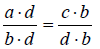so we can than state that
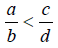if and only if a * d < c * b.
In other words, if the denominators are different , compare their cross products.
Example 1:
Which fraction is greater:
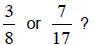
Solution: Let's start by finding equivalent fractions for
both so that they have the same denominator.
Multiply the top and the bottom of 3/8 by 17 and multiply the top and bottom of
7/17 by 8.
This gives us
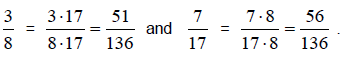
You can see that 7/17 is greater than 3/8 since 56 is greater than 51.
The shortcut method is given in case 2 above.
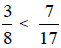because 3 * 17 < 7
*
8.
Example 2:
Which fraction is greater:
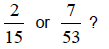
Solution: Since 2(53) > 7(15), 2/15 is greater than 7/53.
**********************************************************************************************************************************
**
Now You Try (Section 4.1)
State which fraction is greater.
(Answers to Now You Try (Section 4.1) are found on page
29.)
**********************************************************************************************************************************
**
Fractions have an interesting property that whole numbers
and integers do not have. If you take two whole
numbers such as 5 and 6, there is not a whole number between them, but if you
are given any two fractions you
can always find another fraction between them. This property is called the
density property.
Example 1:
Find at least one rational number between
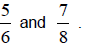
Solution: To find a rational number between
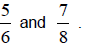you need to find equivalent fractions
for
each so that they have common denominators: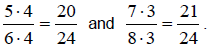 
However, we cannot find a whole number numerator between
20 and 21, so we need to
use a larger common denominator, such as 48: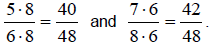 
Since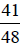 
is between
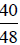and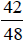 
,
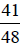is between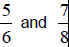 
**********************************************************************************************************************************
**
Now You Try (Section 4.2)
1) Find the fraction between
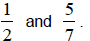
2) Find the fraction between
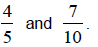
(Answers to Now You Try (Section 4.2) are found on page
29.)
**********************************************************************************************************************************
**
Section 5: Simplifying Fractions to Lowest Terms
By looking at the following examples,
can you think of a way to start with
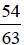and simplify it to get
?
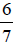To simplify a fraction to lowest terms, we have to divide
the numerator and the denominator by all the factors they
have in common. Recall that factors are numbers that are multiplied together.
When we divide the numerator and
the denominator of a fraction by the same nonzero number, we get an equivalent
fraction. So to simplify a fraction,
all we have to do is recognize what factors the numerator and the denominator
have in common and then divide
the numerator and the denominator by the common factors. Let's do some examples
of simplifying fractions.
Definition: A fraction is said to be in lowest
terms if the numerator and the denominator have no factors in
common other than the number 1.
Example 1:
Write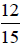 
in the lowest
terms.
Solution: We need to find the factors of 12 and 15
so that we can find one they have in common.
Factors of 12 are: 1, 2, 3, 4, 6, 12
Factors of 15 are: 1, 3, 5, 15
Since 3 is the only factor they have in common, we will divide the numerator and
denominator by 3.
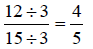In lowest terms, since
4 and 5 have no other factor besides 1 in common.
Example 2:
Write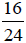 
in lowest terms.
Solution:
Factors of 16 are: 1, 2, 4, 8, 16
Factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24
Since 16 and 24 have 2, 4, and 8 in common, we will choose the highest factor,
8.
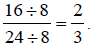In lowest terms, since
2 and 3 have no other factor besides 1 in common.
Notice that you would also write
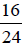in lowest terms, by simply dividing
numerator and
denominator by 2 until they have no factor in common but 1.
**********************************************************************************************************************************
**
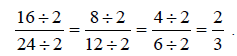
Now You Try (Section 5)
Write the following fractions in lowest terms.
(Answers to Now You Try (Section 5) are found on page 29.
)
**********************************************************************************************************************************
*
| Prev | Next |