Functions
As used in ordinary language, the word function indicates
dependence of a varying quantity on
another. If I tell you that your grade in this class is a function of your
overall average, you
interpret this to mean that I have a rule for translating a number in the range
of 0 to 100 into a
letter grade. More generally, suppose two sets of objects are given: set A and
set B; and
suppose that with each element of A there is associated a particular element of
B. These three
things: the two sets and the correspondence between elements comprise a
function.
| A function f is a mapping from a set D to
a set T with the property that for each element d in D, f maps d to a single element of T, denoted f(d). Here D is called the domain of f, and T is called the target or co-domain. We write f: D → T. We also say that f(d) is the image of d under f, and we call the set of all images the range R of f. |
A mapping might fail to be a function if it is not defined
at every element of the domain, or if
it maps an element of the domain to two or more elements in the range:
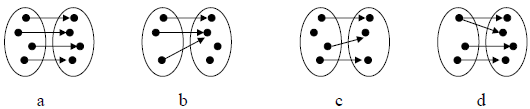
Consider the mappings shown in the diagram above. We note
that examples a and b are both
functions since every element in the first set (the domain) maps to a single
element in the second
set (the co-domain or target). Note that it is fine for two elements in the
domain to map to the
same element in the co-domain (as is the case in b). We point out that
example c is not a function,
since there is an element in the domain which does not map to any element in the
co-domain.
Also, example d is not a function since there is an element in the domain
that maps to more than
one element in the co-domain.
One way to define a function is to provide a table that shows the mapping for
each element of the
domain. For example, in a small class we might have
the set of students S = {Maria, Clara. Tom, Dick, Harry}
the set of possible grades G = {A, B, C, D, NP}
One possible function f: S → G would be:
| d | f(d) |
| Maria Clara Tom Dick Harry |
A B C A B |
The table completely defines the function by showing every
mapping. Note that all the
possible grades are not used, i.e., the range is not the same as the co-domain.
It is still
convenient to call this a function from S to G in order to indicate the
possibilities.
The following table does not define a function from S to G, because not every
member of S is
mapped to a grade:
| d | f(d) |
| Maria Clara Tom Dick Harry |
A B C B |
The following table does not define a function from S to
G, because one member of S is
mapped to two grades :
| d | f(d) |
| Maria Clara Tom Dick Harry Harry |
A B C A B NP |
Another way to define a function to specify a rule for how
the function operates , rather than listing
out the mapping. For example, using the common notations
N: the set of natural numbers {1, 2, 3, ...}
Z: the set of all integers {..., -2, -1, 0, 1, 2, ...}
we could define a function f : N → N with the rule f (a) = 2a. The specification
of the domain and
co-domain are considered to be part of definition, so the function g : Z → Z
where g(a) = 2a is not
the same function as f, even though the rules are the same .
Note that as in the example above, the range of these functions is not the same
as the co-domain.
For example, the range of f is positive even integers, which is not the same as
N. We write
f : N → N to convey the information that everything in the range of f is a
natural number , without
commenting (until we give the rule) on whether every natural number is actually
in the range.
Types of Functions
One-to-One Functions
| A function is called one-to-one, or
injective, if it maps distinct elements of the domain to distinct elements of the range. More formally, a function f is one-to-one if and only if x ≠ y implies that for f(x) ≠ f(y) for all x and y in the domain of f. Another way to say this is that f(x) = f(y) implies x = y. A function is said to be an injection if it is one-to-one. |
For example, the function f: N → N defined by the rule f (x)
= x2 is an injection. However,
the function g: Z → Z defined by the same rule is not an injection, since g(-x)
and g(x) both
map to x2.
Onto Functions
| A function f: A →B is called onto, or
surjective,
if and only if for every element b in B there is at least one element a in A that maps to it, i.e., there is at least one element a such that f(a) = b. Another way to say this is that the range of f is equal to its target. A function is said to be a surjection if it is onto |
For example, the function f(x) = x + 1 from the set of
integers to the set of integers is onto, since
for every integer y there is an integer x such that f(x) = y. By definition, f(x)
= y if and only if
x + 1 = y, implying that x = y – 1. So, for any y, we can find a value x so that
f(x) = y holds.
The function f(x) = x2 from the set of integers to the set of integers is not
onto. This follows from
the fact that there is no integer x such that f(x) = x2 = –1.
One-to-one Correspondence Functions
| A function f is a one-to-one correspondence, or
bijective, if it is both one-to-one and onto. Such a function is called a bijection. |
The function f(x) = x + 1 from the set of integers to the
set of integers is a bijection. It is one-to-
one since x + 1 = y + 1 if and only if x = y. And as we saw above, the function
is onto.
As examples, consider the four functions shown below:
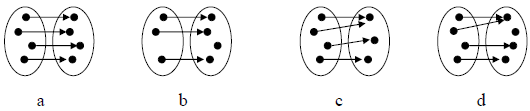 |
Function a is one-to-one and onto (it is a bijection).
Function b is one-to-one, but not onto.
Function c is not one-to-one, but is onto.
Function d is neither one-to-one nor onto.
| Prev | Next |