INTRODUCTION TO MATLAB

Chapter 17
Publication Quality Plots

The default settings which Matlab uses to plot functions are usually fine for looking at plots
on a computer screen, but they are generally pretty bad for generating graphics for a thesis
or for articles to be published in a journal. However, with a bit of coaxing Matlab can make
plots that will look good in print. Your documents will look much more professional if you
will take some time to learn how to produce nice graphics les. This chapter will show you
some of the tricks to do this. This material owes a lot to the work of some former students:
Tom Jenkins and Nathan Woods.

Before getting started, let's review a little about graphics le formats. Raster formats
(e.g. jpeg, bmp, png) are stored as a grid of dots ( like a digital photograph). Raster graphics
are well-suited for on-screen viewing, and they are usually the best choice for graphics
intended for a presentation that will be viewed using a computer projector. However, raster
graphics are usually not a good choice for figures destined for the printer (especially line
plots and diagrams). They usually look blurry and pixelated on paper because of the
mismatch between the image resolution and the printer resolution. Although it is possible
to just make really high resolution raster graphics for printing, it is usually better to use
vector formats for printed line plots and drawings.

Vector formats store pictures as mathematical formulas describing the lines and curves,
and let the renderer (e.g. the printer) draw the picture the best it can. The most common
format used to store vector graphics in physics is encapsulated postscript (EPS). Although
some programs don't display EPS graphics very nicely on screen (Word does a particularly
bad job with on-screen EPS), the figures look great in the printed copy or an exported PDF.
We will first learn how to make nice EPS graphics les for printing, and then later we will
go over some tips for making nice raster graphics for a presentation.

17.1 Creating an EPS File
Matlab can create a vector EPS les for you. To see how this works, let's make a simple
plot with some fake data that looks like something you might publish. Run this example
and then select "Save as..." in the figure window, and Matlab will let you choose to save
your plot in the EPS format. We have included the EPS le generated this way as Fig. 17.1.

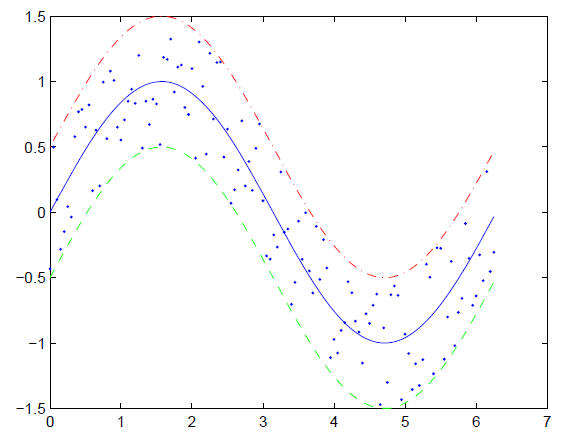
Figure 17.1 Default plot output from Matlab

While this is a pretty simple process , the EPS shown in Fig. 17.1 has a few problems.
The axes Matlab chose on which to plot the function aren't necessarily the ones we would
pick, but back in section 4.7 we learned how to set the limits of a plot, so that can be
addressed (if you don't recall how, go read section 4.7).

A problem that is a little harder to address is that the Matlab default is for figures that
are intended to take up a good fraction of the page. We could just scale Fig. 17.1 to to
be smaller (and we often see this in theses), but the resulting figure often has unreadably
small text and almost invisible lines. This type of figure will not be acceptable for physics
journals. These journals have strict requirements on how wide a figure can be in its final
form because of the two-column format (8.5 cm width) they often use. But at the same
time they require that the lettering be a certain size (for example, American Institute of
Physics journals require that in the final reduced size the lettering be at least 2.8 mm high).
The journals often require that the figures be submitted in Encapsulated Postscript format
(.EPS) that are the right size without any fussing on their part.

While you may not immediately publish in journals, you will almost certainly include
plots in your senior thesis. The rules for figures in your thesis aren't as strict as those for
journals, but you will probably still want to create something that looks nice when scaled
so that the plot doesn't take half a sheet of paper. Fortunately, Matlab allows us to change
the visual properties of a plot . Once you have learned the basics, you can use Matlab to
make suitable figures for your thesis and journal articles.

17.2 Controlling the Appearance of Figures
You can control the visual properties of a figure from the GUI of the figure window. This
capability is great for quick one-time adjustments and to get a feel for what can be done.
To get started, click on the "show plot tools" button on the toolbar to display the interface.
If you haven't used the GUI formatting tools yet, you should take some time to get familiar
with their capabilities. Once you have formatted a figure to your liking, you can save export
an EPS for use in your paper. If you want to control the size of your exported plot through
the GUI, you will need to use the "Export Setup..." option in the File menu before making
the EPS. It is a good idea to save your doctored figure as a . g le (in addition to EPS
le). The . g le stores all of your adjustments, so you can come back later and modify
something and the re-export without having to start from scratch.

As convenient as the GUI interface can be, it has its limitations. Some properties are
buried pretty deep in the interface, and it can get tedious to manually format a large number
of graphs (and then reformat them all when you decide something needs to change).
Fortunately, you can also control the visual appearance of your figures using m- le commands.
With the m- le approach, your plot gets the formatting applied each time you run
your script. You can also cut and paste commands to format all your figures at once after
you've decided on a size and style for your graphics. In the long run, you will save yourself
time by learning to control figure properties from the m- file.

To help you with learn the m- le commands, Matlab allows you to export all of the
adjustments you make to a figure in the GUI to m- le commands using "Generate m-
file..." in the figure's File menu. You can then paste this code into your les to get this
figure formatting each time you run the script. However, before you can make the m- le
formatting commands work as you expect, you need to take the time to understand a few
concepts-just blindly pasting the Matlab-generated code without understanding what it
does will usually not get you what you want. The commands have to be put in the right
place and refer to the right objects. The rest of this section will teach you the basics of how
this works.

Matlab treats a figure as a collection of visual objects. Each object has a handle (a
kind of label) to refer to objects in a figure. A handle is simply a number that Matlab has
associated with an object. (You can look at the number of a handle, but it won't really
tell you anything-it just references a place in the computer's memory associated with the
object.) For most objects, you can get the handle when you create them. For instance, the
code
tt = xlabel('My Label');

stores a handle to the x-axis label object in the variable tt .

Once you have a handle to an object, you can specify the visual properties using the
set, using the following syntax (assuming you have already stored the object's handle in
tt):
set(tt,'PropertyName1','PropertyValue1',...)}

This command tells Matlab to take the object with handle tt and set its PropertyName to
PropertyValue. The last comma and dots are not part of the syntax, but indicate that you
can set as many property Name-Value pairs as you want in the same set command. For
instance, to make the x-axis label 20 point Arial font, you would use the command
set(tt,'FontSize',20,'FontName','Arial');

Take a moment now and modify Example 17.1a to add an x-axis label and change its font
size to 8 point.

One of the most frequently referenced objects is the axes object. This object includes
the box surrounding the plot, and it also includes all the labels and titles as child objects.
When you set many of the properties of the parent axes object (e.g. the font size), the child
objects also inherit this setting. This feature makes the axes object a useful way to set a
bunch of things at once. Getting a handle to an axes object is a little different because you
don't usually create axes objects manually-Matlab usually does it for you (for instance,
when you use the figure command Matlab makes an axes object to put in the figure). To
get a handle to an axes object, you use gca command (which stands for Get Current Axes).
For instance, the command
aa = gca;

stores the handle for the current axes object in the variable aa. You need to use gca to
store the current handle in a variable before you open another set of axes (e.g. by using the
figure command), otherwise the axes you want to refer to will no longer be the current
axes. If, for example, to want to set the font to 12 point Symbol for a figure , you would use
set(aa,'FontSize',12,'FontName','Symbol');

See "Axes Properties" in the online help for a list of properties you can set for the axes.

Another frequently used object is the lineseries object, which refers to the lines or
symbols displayed inside an axes object to represent the data. Matlab can have multiple
lineseries plotted on the same set of axes, so we need a way to reference an individual
lineseries independent from the axes on which they are displayed. Take a moment to
modify the code in Example 17.1a to get handles to the individual lineseries objects using
the following syntax:
pp = plot(x,f,'b',x,data,'b.',x,err_hi,'r-.',x,err_low,'g--');

This syntax stores an array of handles referring to the lineseries objects displayed by the
plot command in the variable pp. The first element, pp(1), refers to the first lineseries
(the plot of f), the second element, pp(2), refers to the second lineseries (the plot of data),
and so forth.

The syntax for setting the properties of the lineseries object is essentially the same as
the axes, except you use the handle to the lineseries:
set(pp(1),'PropertyName1','PropertyValue1',...)}

Again, you can set as many lineseries properties as you want in the same set command. To
get the hang of this, modify Example 17.1a again to change the plot of the data variable
to red stars rather than blue dots using the following command:
set(pp(2),'LineStyle','none','Marker','*','Color',[1 0 0])

Note that here we have chosen to set the color with an RGB value rather than a preset
color (an RGB value is a matrix of three numbers between 0 and 1 which specify a color).

Because we often need to control the visual styles of the lineseries data, Matlab gives us
shortcuts to set many of the visual properties of the plot data right in the plot command.
You have have already learned many of these (and in fact we used some in our example).
You could have gotten the red star effect simply by changing your plot command to
pp = plot(x,f,'b',x,data,'r*',x,err_hi,'r-.',x,err_low,'g--');

You can also set properties that apply to every lineseries in the plot by putting name-value
pairs at the end of a plot command. For example, change your plot command in
Example 17.1a to
pp = plot(x,f,'b',x,data,'r*',x,err_hi,'r-.',x,err_low,'g--','LineWidth',2);

Note that this changes the line thickness for the plots to a heavy 2 point line (the default
width is 0.5 point). However, the stars are also drawn with heavy lines which looks kind
of awkward. If you want to control the properties of the lines individually, you have to go
back to the longer syntax with handles. For example
pp = plot(x,f,'b',x,data,'r*',x,err_hi,'r-.',x,err_low,'g--');
set(pp(1),'LineWidth',2);

makes the plot of f heavy, but leaves the rest at the default width. See "lineseries properties"
in the online help for a list of properties you can set for a lineseries.

17.3 Controlling the Size of Exported Graphics
Controlling the size of the exported figure is tricky. The basic idea in controlling size is
that you have the OuterPosition property which specifies the extent of the entire figure,
the Position property which specifies the position of the axes box within the figure, and the
TightInset property that describes the size of the labels around the axes box. If you want
to learn about these properties, see "axes properties" in the Matlab help. Probably the
best way to learn how to do this is to study an example. Execute Example 17.2a and see
what the plot looks like. The EPS produced using "Save As" is included as Fig. 17.2 in this
document so you can see what was affected by these commands ( compare with Fig . 17.1
which shows the output without the sizing commands).

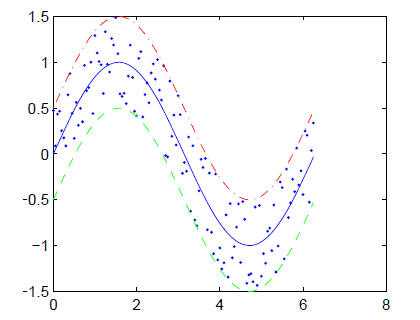
Figure 17.2 Plot made in Example 17.3a (no scaling).