Macroeconomics Midterm 2
Instructions
1.This is closed book, closed notes exam.
2.No calculators of any kind are allowed.
3. Show all the calculations .
4.If you need more space, use the back of the page.
5.Fully label all graphs .
Good Luck 
1.(10 points). Suppose you deposit $x in a savings account
that pays interest of i%
per year. Write the equation that gives the amount of your savings after t years
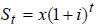
2.(10 points). If a variable grows at constant rate, then
the natural log of the variable
is
a. Increasing function of time
b. Decreasing function of time
 Linear function of time
Linear function of time
d. Quadratic function of time
e. Impossible to tell without more information
3.(15 points). The next table provides data on prices and
output in some artificial
economy for the years 2000 – 2002. The goods are labeled 1 and 2, so that
P1, P2,Q1,Q2 are prices and
quantities of the two goods respectively.
| Year | P1 | Q1 | P2 | Q2 |
| 2000 | 2 | 50 | 30 | 5 |
| 2001 | 3 | 57 | 30 | 19 |
Calculate the inflation rate between the years 2000 and
2001, using 2001 as the
base year.
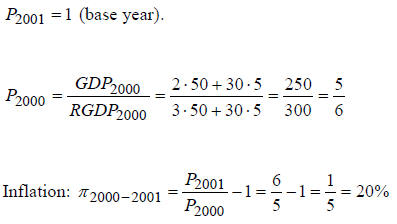
4.(30 points). Suppose that consumer's utility function is
u(x,y). The prices of
goods X and Y are PX,PY, and his income is I.
a. Write the consumer's problem.
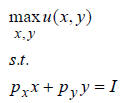
b. Write the mathematical condition for optimality of
consumption bundle
and give a verbal interpretation of it.
The condition for optimal consumption bundle:
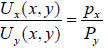
Interpretation 1: The left hand side is the slope (in absolute value) of
the indifference
curve and the right hand side is the slope of the budget constraint. Thus, at
the optimum,
the indifference curve is tangent to the budget constraint.
Interpretation 2: The above condition can be written as
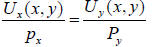
The left hand side is the utility generated by extra
dollar spent on X and the right hand
side is the utility from extra dollar spent on Y. The optimal allocation of
income between
the two goods requires that those should be the same.
c. Suppose that the utility function is u(x,y)=x3y6.
Circle the correct
statement.
i. The consumer will spend 50% of his income on the good X
ii. The consumer will spend $3 on good X and $6 on good Y
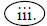 The consumer will spend 1/3 of his income on
good X
The consumer will spend 1/3 of his income on
good X
iv. The consumer will spend all his income on good Y
5.(20 points). Suppose that a firm has technology given by
Y=F(K,L), the price
of the final good (Y) is P, and the prices of inputs are R,W The firm is a price
taker in market for final good as well as the markets for inputs.
a. Write the firm's optimization problem.
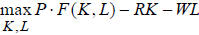
b. Derive the first order conditions for your problem in
a, and provide a
verbal interpretation of it.
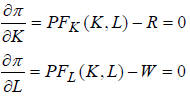
Competitive (price taking firm) will hire inputs up to the point when their
marginal
product equals their prices.
| Prev | Next |