MATH 104 Midterm Test Solutions
| Problem | Possible score | Average score |
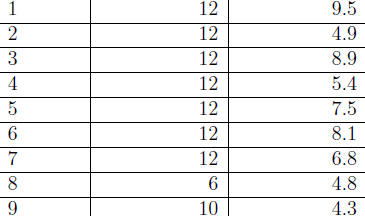 |
||
| Total |
100 |
60.2 |
1. (12 points) Find 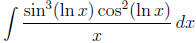 .
.
Let u = ln x. Then the integral becomes
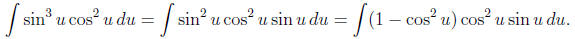
Substitute t = cos u to get
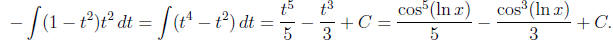
2. (12 points) Find 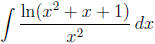 .
.
Do integration by parts with u = ln(x2 +x+1) and dv = dx/x2. Then du = (2x+1) dx/(x2
+x+1)
and v = −1/x. So
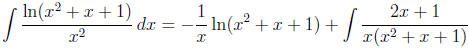
Now use partial fractions to compute the integral on the right.
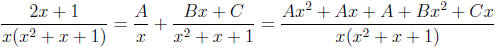
This leads to 0 = A + B, 2 = A + C, 1 = A and we conclude that B = −1 and C = 1.
So now we
have
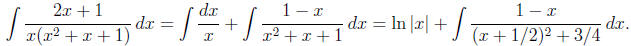
In this integral we make the substitution u = x + 1/2 and then −u + 3/2 = −x + 1. So we get
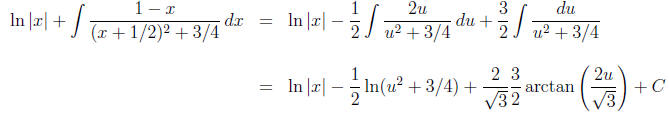
Returning to the original variable x and combining all the pieces gives
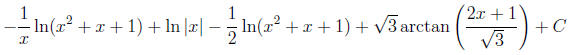
3. (12 points) Find 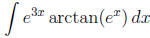 .
.
Start with a substitution w = ex. Then dw = ex dx. We get
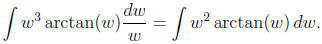
Now do integration by parts, with u = arctanw and dv = w2 dw. So du = dw/(1+w2) and v = w3/3.
Thus our integral becomes
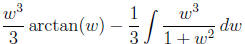
Long division gives w3/(1 + w2) = w − w/(1 + w2) so we have
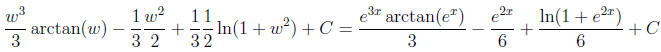
4. (12 points) Find 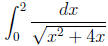
Complete the square : x2 + 4x = (x + 2)2 − 4 and make the substitution u = x + 2 to get
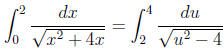
Now make the substitution u = 2 sec θ . The integral becomes
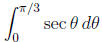
since du = 2 sec θ tan θ dθ , u2 − 4 = 4 tan2θ. In addition u =
2 corresponds to sec θ = 1 or θ = 0 and
u = 4 corresponds to sec θ = 2 or cos θ = 1/2 or θ = π
/3.
Continuing the integration
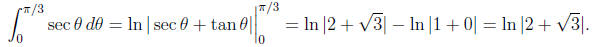
5. (12 points) Find 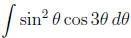 .
.
Replace sin2θ by (1 − cos 2 θ)/2 to get
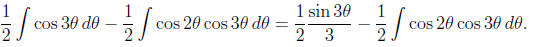
Either using the formulas in the text or using the addition formula for cosine we find that
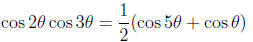
Thus
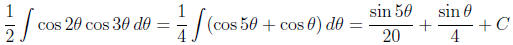
Putting all the pieces together our answer is
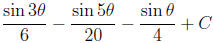
6. (12 points) Set up an integral for the area of the
region enclosed between the curve y = x3 − 2
and its tangent line at x = −1. JUST SET UP THE INTEGRAL. DO NOT COMPUTE A
NUMERICAL VALUE .
First we have to find the tangent line at the point (−1,−3) on the cubic curve .
The slope is
dy/dx = 3x2 evaluated when x = −1. So the slope is 3. The line of slope 3
through the point
(−1,−3) turns out to be the line y = 3x.
If we sketch the graphs, it is clear that the tangent line lies above the cubic.
So our top curve is
y = 3x and the bottom curve will be y = x3 − 2. We need to find the points where
the tangent and
the cubic intersect. Of course one intersection is at x = −1. To find the other
one we set the two
curves equal, and using the fact that x = −1 is a root we know that x + 1 should
be a factor of the
cubic equation we get. Long division then lets us find the other root.
x3 − 2 = 3x => x3 − 3x − 2 = 0 => (x + 1)(x2 − x − 2) = 0 => (x + 1)(x + 1)(x − 2)
= 0
So the other intersection is at x = 2. So the integral we want is
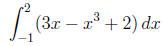
7. (12 points) The region R is bounded by the curves y =
ln x, y = 0 and x = e. The solid S is
obtained by revolving R around the y-axis.
(a) Set up an integral for the volume of S using the shell method .
We slice the region vertically as x runs from 1 where the graph of y = ln x
crosses the x-axis
up to x = e, a given boundary curve for the region. The slice at x has length ln
x. We rotate
about the y axis, so the radius is x. Thus
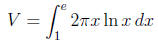
(b) Set up an integral for the volume of S using the disk
or washer method.
Now we have to slice horizontally. The slice at height y runs from the graph of
y = ln x to the
vertical line x = e. This horizontal slice will generate a washer. The outer
radius will be e and
the inner radius (the radius of the hole in the center) will be x = ey. We slice
as y runs from 0
to 1. So our integral is
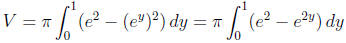
(c) Compute the volume of S. If we use the shell integral we compute using integration by parts.
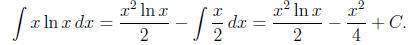
Evaluating between 1 and e we eventually get
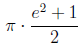
using the fact that ln e = 1 and ln 1 = 0.
8. (6 points) Sketch the curve given in polar coordinates by r = 1 + sin θ.
As runs from 0 to π /2 we move through the first quadrant in a counterclockwise
direction and r
increases steadily from 1 to 2. As we move through the second quadrant, r
decreases in a completely
symmetric fashion from 2 back to 1. As we swing through the third quadrant, the
r values continue to
steadily decrease, reaching the value 0 as θ reaches 3π /2. So the curve curls into
the origin, tangent
to the the θ = 3π /2 ray (the negative y -axis). In a symmetric way, as we swing
through the fourth
quadrant, the r values increase from 0 to 1, so the curve comes out of the
origin, again tangent to
the negative y-axis.
The resulting curve is a cardioid that crosses the positive x -axis at 1, the
positive y-axis at 2, the
negative x-axis at −1 and has a cusp at the origin, centered on the negative
y-axis.
9. (10 points) Find the length of the curve 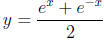 as x runs from 0 to 1.
as x runs from 0 to 1.
Parametrize the curve as 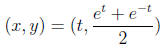
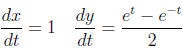
So we need to compute 1 + (dy/dt)2:
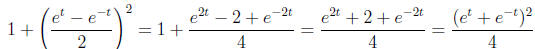
Thus the speed is
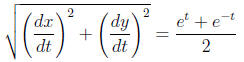
So the arclength is
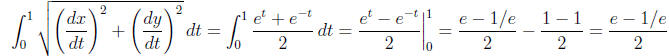
| Prev | Next |