Math 111 Sections 6 and 7

1. (20 points) Tell whether or not the following sentences are statements. Of the
sentence is not a statement, explain why not.

 (a) The television is turned on.
 (b) The Grand Canyon is the most spectacular sight in the world
 (c) Do you want to do out next Friday?
 (d) It snowed until 12am last Saturday night.
 (e) The mathematics department at UK is located on the seventh floor of Patterson Office Tower.

Solution :
 a) statement
 b) not a statement–this is an opinion
 c) not a statement–this is a question
 d) statement
 e) statement

2. (10 points) Consider the expression n ^2 − n + 3. If whole number values (i.e.,
0, 1, 2, . . .) are substituted in for n , explain why induction would lead you to conclude
that this is a prime number generator . What is the first number that gives a non-prime
result?

Solution :
If we substitute in n = 0, n = 1, and n = 2, the results are all prime. Induction would lead
us to conclude, from these observations, that the expression is a prime number generator.
However, for n = 3, 3^2 − 3 + 3 = 3^2 = 9 = (3)(3), which is non-prime.

3. (15 points) Consider the following argument:
If the U.S. bombs Iran to destroy the country’s nuclear facilities, then many other countries
in Europe and the Middle East will be angry at our government. Many other countries in
Europe and the Middle East are already angry at our government. Therefore we should
bomb Iran to destroy the countries nuclear facilities.

 (a) Convert the above argument into symbolic form and draw the corresponding diagram.
 (b) Is the above argument a correct argument? Justify your answer by using
the definition of a correct argument (i.e., do not use a truth table).

Solution :
 a) Let A be the statement ”the United States bombs Iran, etc.” and B be the statement
”other countries are mad at the U.S.”

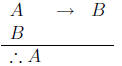
 b) The argument is not correct since it is not one of our three correct argument forms,
affirming the antecedent, denying the consequent, and hypothetical syllogism.

4. (25 points) Let A be the statement ”Chloe is taking MA111” and let B be the
statement ”Chloe is taking MA109”.

 (a) Write out, in words, the negation of A and the negation of B.
 (b) Write out, in words,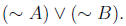
 (c) When is 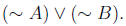true? That is, use a truth table to find out for
which values of A and B is 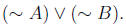true.

Solution:
a)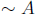 = Chloe is not taking MA111.
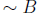= Chloe is not taking MA109.
b) Chloe is not taking MA109 or MA111. c)

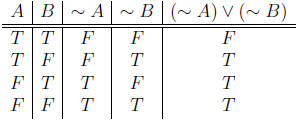
5. (10 points) Give an example, if possible, of each of the following. If the example is
not possible, explain why.

 (a) Natural Number
 (b) Whole Number
 (c) A rational number that is not an integer.
 (d) A real number that is not a rational number.
 (e) A natural number that is not a real number

Solution:

 a) 1, 2, 3, ...
 b) 0, 1, 2, 3, ...
 c) 1/2

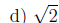
 e) not possible since all natural numbers are real numbers

6. (20 points) Prove that hypothetical syllogism is a correct argument by using a truth table.

(Recall that a hypothetical syllogism is an argument of the form:

A implies B
B implies C
Therefore, A implies C.

First convert the argument into symbolic form and then do its truth table.)

Solution:
Since the argument is of the form

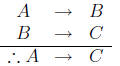
We are doing the truth table of

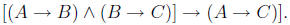
Since the last column is all true, the argument is correct.