MATH 115A - Lecture 4 Midterm 1

STUDENT ID #:

This is a closed-book and closed-note examination.
Calculators are not allowed .
Please show all your work.
Use only the paper provided. You may write on the back if you need more
space, but clearly indicate this on the front.
There are 5 problems for a total of 100 points.

POINTS:

1.
2.
3.
4.
5.

1. (10 points each) For the given subset W of the F-vector space V ,
prove or disprove that W is a subspace of V .

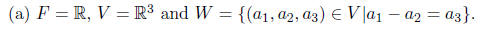
Clearly, the zero vector (0, 0, 0) is in W. Now suppose a = (a₁, a₂, a₃) and
b = (b₁, b₂, b₃) are in W. Then (a₁+b₁)-(a₂+b₂) = a₁-a₂+b₁-b₂ = a₃+b₃,
so a + b ∈W. If 2 R is a scalar, then λa₁ - λa₂ = λ(a₁ - a₂) = a₃, so
a ∈W. That is, W is closed under addition and scalar multiplication and
contains 0, hence, it is a subspace.

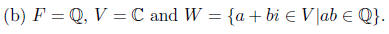
The two complex numbers x = 1 and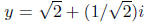 are both in W.
However, 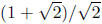is not rational , so that x + y is not in W. That is,
W is not closed under addition and is therefore not a subspace.

2. (20 points) Let 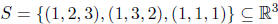. Is S a basis of
R³? If so, prove it. If not, disprove it.

Because the dimension of R³ is 3, it suffices to show either that S is linearly
independent, or that S is a generating set. Either is easily accomplished by
solving linear equations .

3. (20 points) The set of complex numbers C can be viewed as both an
R-vector space and a C-vector space. Give an example of a map T : C -> C
that is R-linear, but not C-linear.

For example, the map T : C -> C defined by T(a + bi) = a is easily
checked to be R-linear, but not C-linear. First, we check that T is additive.
Let x = a + bi and y = c + di be two complex numbers . Then T(x + y) =
T((a + c) + (b + d)i) = (a + c) = T(x) + T(y).

Next, let λ ∈R be a real scalar , and x = a+bi a complex number. Then
T(λx) = T((λa) + (λb)i) =λa =λT(x). Thus, T is R-linear.

Finally, we show T is not C-linear. Let x = i ∈C (element of the vector
space) and = i ∈C ( complex scalar ). then T(λx) =-1, but λT(x) = 0.

4. (20 points) Let D : C¹(R) -> C(R) be the map on continuously
differentiable functions given by the derivative, that is, D(f)(x) = f'(x).
Show that D is linear (you may assume what you know from calculus) and
give a basis for the Null space (that is, the kernel) of D.

Let f and g be elements of C¹(R), and let c ∈R be a scalar. Then
D(cf + g) = D(cf) + D(g) = cD(f) + D(g), where the first equality holds
because the derivative of a sum is the sum of derivatives, and the second
because the derivate of a multiple is the multiple of the derivative. This
shows that D is a linear transformation .

The Null space of D is the set of all continuously differentiable functions f
such that f'(x) = 0 for all x ∈R. Such function are the constant ones, that
is, 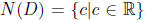A basis for this space is any one constant non-zero
function, for example,

5. (20 points) Let V be the R-vector space of functions in one variable x
of the form 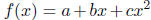where a, b and c are arbitrary real numbers .
Define a map 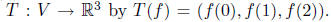Show that T is a
linear transformation and determine the dimension of its Null space N(T)
and its range R(T).

Let f and g be in V , and let c ∈R be a scalar. Then T(f + g) =
((f +g)(0), (f +g)(1), (f +g)(2)) = (f(0)+g(0), f(1)+g(1), f(2)+g(2)) =
(f(0), f(1), f(2))+(g(0), g(1), g(2)) = T(f)+T(g) and T(cf) = ((cf)(0), (cf)(1), (cf)(2)) =
(cf(0), cf(1), cf(2)) = c(f(0), f(1), f(2)) = cT (f). That is, T is a linear
transformation.

We compute the range of T. I claim T is onto. To show that, it suffices to
give elements f, g and h in V such that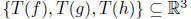is a basis.
Let f(x) = x(x-1)/2, g(x) = -x(x-2) and h(x) = (x-1)(x-2)/2. Then
T(f) = e₁, T(g) = e₂ and T(h) = e₃. Thus, T is onto and the dimension of
the range is 3.

Since the dimension of V is equal to the dimension of R³, the dimension
theorem implies that the dimension of the Null space is 0.