Math 140 P2 Exam #2 Solutions
1. Factor each polynomial completely .
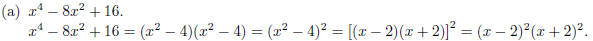
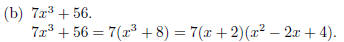
2. Perform the indicated operations . Leave your answer in factored form.
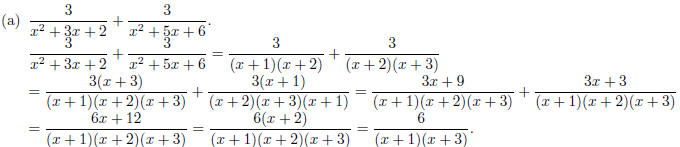
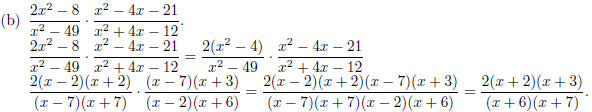
3. Solve the equation 2x2 − 8x + 4 = 0 by
completing the square.
2x2 − 8x + 4 = 0 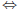 2x2 −
8x = −4
2x2 −
8x = −4
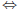 x2 − 4x = −2.
x2 − 4x = −2.
So, m = −4, 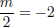 , and
, and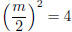 .
Hence, we have
.
Hence, we have
x2 − 4x + 4 = −2 + 4 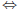 (x − 2)2
= 2. By the square root method
(x − 2)2
= 2. By the square root method
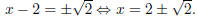
The solution set is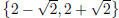 .
.
4. Solve each of the inequalities , and graph their solution set.
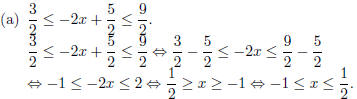
Interval notation: 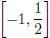

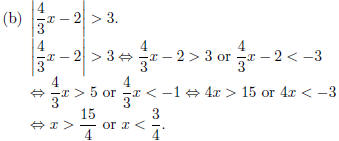
Interval notation: 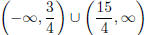 .
.

5.Find all real solutions to the following equations.
(a) |3x − 5| = 17.
Either 3x − 5 = 17 or 3x − 5 = −17
![]() 3x = 22 or 3x = −12
3x = 22 or 3x = −12
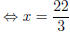 or x = −4. Solution set:
or x = −4. Solution set: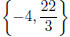 .
.
(b) x(3x − 7) = −1.
x(3x − 7) = −1 ![]() 3x2
− 7x = −1
3x2
− 7x = −1 ![]() 3x2
− 7x + 1 = 0.
3x2
− 7x + 1 = 0.
Using the quadratic formula .
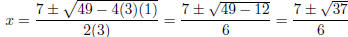 Solution set:
Solution set:
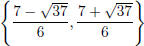 .
.
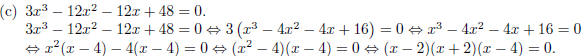
By the zero - product property , either x = 2, x = −2, or x = 4.
Solution set: {−2, 2, 4}.
(d) |x2 − 7x + 6|= 6.
Either x2 − 7x + 6 = 6 or x2 − 7x + 6 = −6.
![]() x2 − 7x = 0
or x2 − 7x + 12 = 0
x2 − 7x = 0
or x2 − 7x + 12 = 0
![]() x(x − 7) = 0 or (x −
4)(x − 3) = 0.
x(x − 7) = 0 or (x −
4)(x − 3) = 0.
By the zero- product property , either x = 0, x = 7, x = 3, or x = 4.
Solution set: {0, 3, 4, 7}.
6. Express the following complex numbers in the standard form a + bi.
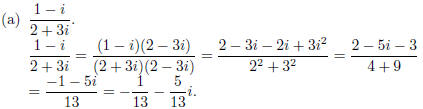
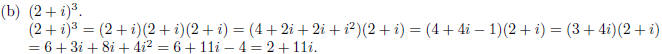
7. Solve the following equations over the complex numbers .
(a) 5x2 + 2 = −3x.
5x2 + 2 = −3x
![]() 5x2 + 3x +
2 = 0. Using the quadratic formula,
5x2 + 3x +
2 = 0. Using the quadratic formula,
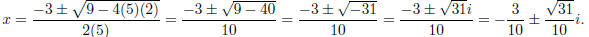
Solution set: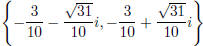 .
.
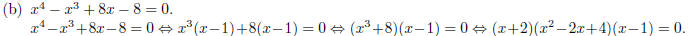
By the zero- product property , either x = −2, x = 1, or x2 −2x+4 = 0.
Use the quadratic formula
on x2 − 2x + 4 = 0 and get
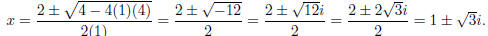
Putting everything together, we have x = −2, x = 1, or
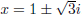 . So the solution set is
. So the solution set is
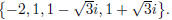
8. Extra Credit Solve x6 − 1 = 0 over the
complex number system. (Suggestion: Factor using the difference
of squares to get started.)
x6 − 1 = 0
![]() (x3 − 1)(x3 + 1) = 0
(x3 − 1)(x3 + 1) = 0
![]() (x − 1)(x2
+ x + 1)(x + 1)(x2 − x + 1) = 0. Using the quadratic
(x − 1)(x2
+ x + 1)(x + 1)(x2 − x + 1) = 0. Using the quadratic
formula on x 2 + x + 1 = 0, we get 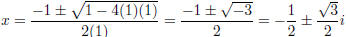
Using the quadratic formula on x 2 − x + 1 = 0,
we get
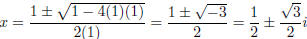
Solution set: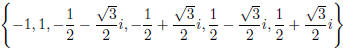 .
.
| Prev | Next |