MATH 185 EXAM #2
1. The theorem of the mean policeman. Consider the following situation.
“Jimmy is hungry and decides he wants food at Tim’s drive-in which is in a town
exactly
30 miles away (in a straight line), we will call this town X. The only road
between these
two towns has a speed limit of 50mph. He gets in his ’57 mustang convertible and
drives
to town X, picks up lunch at the drive-in and then drives home. The local
sheriff notices
Jimmy leave town at 12:30pm. He notices Jimmy return at 1:30pm, this time
carrying a
bag with a half-eaten hamburger from Tim’s drive-in. As soon as Jimmy parks his
car, the
sheriff walks over to Jimmy and writes him a ticket for speeding by 10mph.”
Give a mathematically rigorous explanation which proves that the sheriff is
correct in
assuming that Jimmy was speeding by at least 10mph at some instant. You may
assume
that the function J (t), which gives the total distance that Jimmy has driven
since leaving
town, is differentiable. (5 points)
Proof. We assume t is in hours. Note that J(0) = 0 and that J(1) = 60. Thus
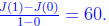
By the “mean” value theorem , there exists a t 0∈ (0, 1) such that
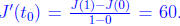
This completes the proof. If one wants to argue something about Jimmy’s average
velocity,
and one wants to make it rigorous, one needs to make some kind of argument about
integrals
or at least areas under curves .
2. Prove that the function
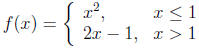
is differentiable at x = 1. (5 points)
Hint: You may use the fact that a limit exists whenever the left and right
limits exist and
agree.
Proof. There are a number of correct ways to do this problem. We’ll do a short
one here.
Note that regardless of anything else, we know that f' is defined for x ≠ 1. We
see that
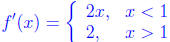
But then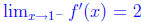
and
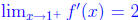because polynomials and constant
functions
are continuous. By a Theorem at the end of section 3-21, we see that f is
differentiable
at x = 1.
3. Let f : R → R be a function with a third derivative and
suppose that there exists x 0∈ R
so that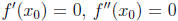 
and
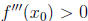. Show that there exists
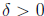so that f is
increasing on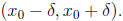 
(10 points)
Hint: What does the graph of f' look like at x = x0 (a graph is not a
rigorous proof
however).
Proof. Note that f' (x) is concave up at x0. Thus there exists 
such that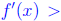 
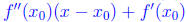for all 
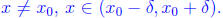Plugging values in, we see that
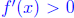for all
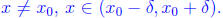Since
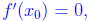we see that on the interval
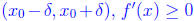and furthermore that
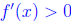except at a finite number of points.
By a theorem in section 3-21, this proves that f (x) is increasing.
4. Consider the parametric equation
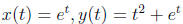
(a) Calculate the value of
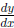for t = t0. (3 points)
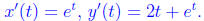Thus d
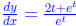At
t0 we get
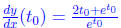
(b) Write down a formula for the tangent line to the graph
at the point t = t0. (2 points)
We know y = m x + b, so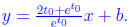 
The line goes through
(x(t0), y(t0)), so
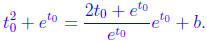
Solving for b we get
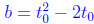
and so our final equation is
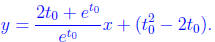
(c) What value of t0 in the interval [0, 3] minimizes the y-intercept
of tangent line you just
wrote down. Justify your answer (5 points).
Hint: Recall that the y- intercept of a line written in the form y = m x + b is
simply the
value of b.
We view b as a function of t0 and so we write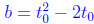
(Note that now t0 is actually
a variable , and not a constant).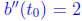 
, so that b
is concave up.
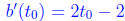and so
we see the only critical point is at t0 = 1. This is in the interval
[0, 3] and by the second
derivative test, it must be a local min. Therefore, it is the absolute minimum
by a theorem
from chapter 6.
(EC) Suppose that f : R → R is twice differentiable and
one-to-one. Further suppose that
f'' (x) > 0 for all x ∈ R and that f is a monotonically increasing function and
that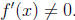 
Show that f -1 is concave down. (5 points)
Proof. Since f is twice differentiable, f' is differentiable, and thus
continuous. Therefore
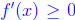(because if it was < 0, it would be <
0 on some interval, and thus it would be
decreasing). But this implies, because 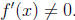that
f' (x) > 0.
Now we know that
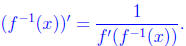
Taking another derivative (using the chain rule) we see that
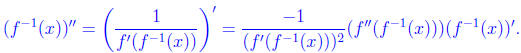
Plugging in our formula for
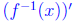yet again, we see that
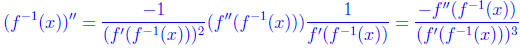
Now, f'' of anything is always positive , as is f', so
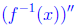= −(positive)/(positive)
and thus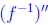
is negative
for all x, so that f -1 is concave down.
(EC) Suppose that f : R→ R is twice differentiable.
Further suppose that f'' (x) < 0 for all
x ∈ R. Prove that for each real number L, the equation L = f (x) has at most two
solutions.
(5 points)
Hint: Analyze the solutions to the equation f' (x) = 0.
Proof. Suppose that L = f(x) has at least three different solutions, we will
prove a contradiction.
Let us label x1 < x2 < x3 as three of the
solutions. Since f(x1) = f(x2), by
Rolle’s theorem, we see that there exists a x4 ∈ (x1, x2)
such that
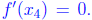Likewise,
there exists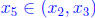 
such that
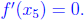Now, since f'' (x) < 0, f' (x) is
monotonically
decreasing and thus f' is one to one. However,
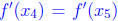(since they are both zero )
and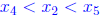 
which demonstrates that
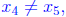, which is a contradiction.
Remark 0.1. It is possible to do a careful and correct by first showing that f'
can cross zero
at most once. Furthermore, the sign of f' changes only at that point (if it
exists) because
f' is continuous (essentially by the intermediate value theorem). Then one can
analyze the
cases where f' < 0 and f' > 0 individually, and make the same conclusion.
| Prev | Next |