Math 441 Assignment 8 Solutions
1. [2 points] List the elements of the group U 20.
U20 is the set of units in Z20, which are the elements [a] ∈Z20
which are relatively
prime to 20. Then
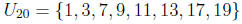
2. (a) [2 points] Show that the composition of two injective functions is
injective.
Suppose g : A -> B and f : B -> C are injective functions. Then suppose
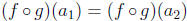for some
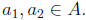Then
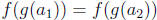and
since f is injective, that means that
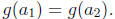Since g is also injective,
this means that a1 = a2.
Then the composition 
is injective.
(b) [2 points] Show that the composition of two surjective
functions is surjective.
Suppose g : A -> B and f : B -> C are surjective functions, and let
c ∈C. Since f is surjective, there is some b ∈B such that f(b) = c.
Since g is surjective, there is some a ∈A such that f(a) = b. Then
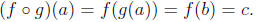
Then the composition is surjective.
(c) [4 points] Let T be a nonempty set and let A(T) be the
set of all permutations of
T. Show that A(T) is a group under the operation of composition of functions.
(You may assume that a bijective function has an inverse that is bijective.)
A permutation in A(T) is a bijection (injective and surjective function)
from T to T.
•A(T) is closed under composition: Let f : T -> T and g :
T -> T
be two permutations in A(T). Then both f and g are bijective and
by parts (a) and (b), their composition 
: T
-> T is a bijective
function. So A(T) is closed under composition.
•Composition of functions is associative: Let f, g, h ∈A(T).
Then, for
any t ∈T,
•The identity element in A(T) is the identity function
id(t) = t for all
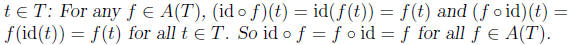
•If f is in A(T), then f is a bijective function from T to T and has
an inverse f-1 from T to T which is also a bijective function. So
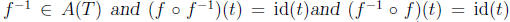for all
t∈T. So for any f∈A(T), there is an element f-1∈A(T) such that
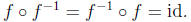
3. [10 points] Let 1, i, j, k be the following matrices with complex entries :
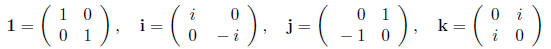
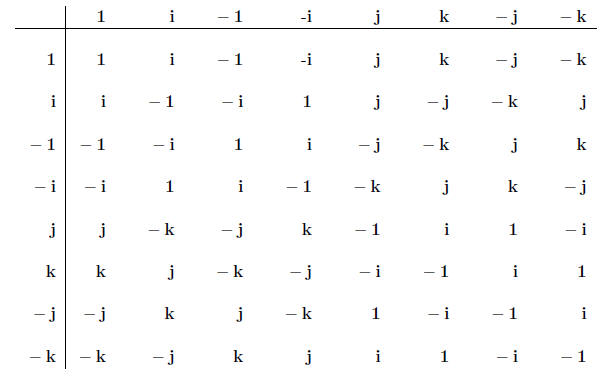
Show that Q = {1, i,-1,-i, j, k,-j,-k} is a group
under matrix multiplication by
writing out its multiplication table . Q is called the quaternion group.
| Prev | Next |