Math Review
I. This is calculus-based physics
A. but good algebra skills are very important
1. We’ll actually do a lot more algebra than calculus
B. You’ll also need to remember some geometry and trigonometry
C. So, we’ll have a quick math review …
II. Algebra
A. Manipulating equations
1. Do algebra, and save the number-crunching for last
a) minimize button-pushing errors on calculator
b) easier to track units on numbers and make sure the units come out correctly
(more later)
2. Example: solve this equation for “a”
a)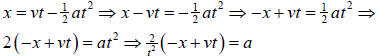
B. Solving simultaneous equations
1. Example: what are x and y in 4x-y=5 and 3x+2y=12 ?
a) Method 1:
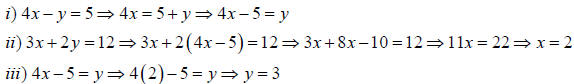
b) Method 2:
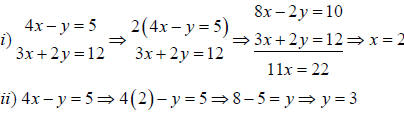
C. Solving quadratic equations
1. Quadratic equation: variable raised to power of 2
a) x2-x-6=0
2. Factoring a quadratic equation
a) Put the equation in the form
(x +a) (x +b)=0
(1) or x2+ax+bx+ab=0 ⇒x2+(a+b)x+ab=0
(2) We need the factors of -6 such that
(a) they equal -6 when multiplied together
(b) and they equal -1 when added together
(3) Factors are: (-1,6), (1,-6), (2,-3), (3,-2)
(a) only (2,-3) satisfies both requirements
b) So the result is (x+2)(x-3)=0
(1) and the possible values for x are
x +2=0⇒x=-2
x-3=0⇒x=3
3. Using the quadratic formula
a) The quadratic formula is a general solution to the quadratic equation
ax2+bx+c=0
(1) quadratic formula is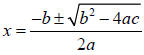 
(2) Two answers (due to ±) – which is the one we want?
(a) In physics, one answer will often “make sense” more than other
(b) The correct choice may depend on the question being asked
b) Example: 3x2+5x-2=0
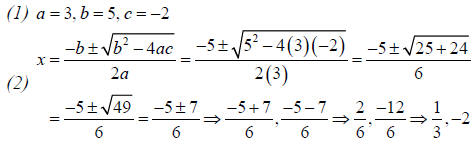
III. Geometry
A. Areas and volumes of geometric shapes
1. Rectangle (square): A=l*w, P=2l+2w
2. Triangle: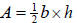
3. Circle: P=π*d=2πr,
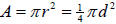
4. Box (cube): V=l*w*h, A=sum of areas of faces
5. Sphere: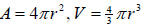
6. Cylinder: A
lateral
=2πr*h, A
total= A
lateral+2(πr2), V=πr2h
IV. Trigonometry
A. Degrees and radians
1. units for measuring angles
a) Make sure you have your calculator set in the
correct mode!
2. Moving in a complete circle goes through 360° or 2π radians
a) hence, to convert between them:
(1) degrees to radians: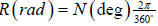
(2) radians to degrees: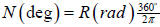
3. Right angles are 90° (π/2 rad)
4. The three angles in a triangle sum to 180° (π rad)
B. Measuring angles on a Cartesian plot
1. We’ll frequently specify the direction of a line , relative to the Cartesian
(x-y) axes
2. The most common method is measuring CCW from the +x axis
a) e.g., illustrate 30°, 45°, 90°, and 180°
b) measuring CW is the negative direction: -60° (300°), -120° (240°)
3. Another method is relative to cardinal directions (N,S,E,W)
a) 20° W of N, 30° S of E, due south, etc.
C. Trig functions
1. Sine, cosine, and tangent
a) Defined relative to the sides of a right triangle
(1) two “regular” sides and the hypotenuse (opp. the right
angle)
(2) Sine: opposite side over the hypotenuse
(3) Cosine: adjacent side over the hypotenuse
(4) Tangent: opposite side over adjacent side
(5) Useful mnemonic: Soh-Cah-Toa
b) Useful trig identities (consult a math handbook!)
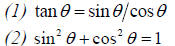
2. Some special right triangles
a) 1,2,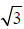
right triangle (a 30° angle and a
60° angle)
b) 1,1,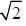
right triangle (two 45° angles)
| Prev | Next |