matrix operations
1 Algebraic properties of matrix operations
1.1 Properties of matrix addition
| Let A, B, C be m× n matrices | Let a ,b, c be any numbers | |
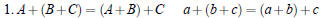 |
Associative | |
 |
Commutative | |
| 3. A+ O = A, where O = [0] is the zero matrix . |
a+0 = a. | Additive identity |
| 4. A+(−A) = O, where −A = [−aij ] is the negative of A. |
a+(−a) = 0. | Additive inverse |
1.2 Properties of matrix multiplication
| Let A, B, C be appropriate matrices | Let a ,b, c be any numbers | |
| 1. A(BC) = (AB)C | a(bc) = (ab)c | Associative |
| 2. A(B+ C) = AB+ AC C(A+ B) =CA+ CB |
a(b+ c)=ab+ ac =(b+ c)a | Distributive |
| AB may not be BA | ab = ba. | Commutative |
| 4. AI = IA = A, only for square matrices, I is called the idetity. |
a 1 = a | Mult. identity |
| 5. A−1 exits only when they are invertible |
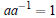 |
Mult. inverse |
Example. Example 10 page 39, pblm 32 page 41.
1.3 Properties of scalar multiplication
Let r, s ∈R and A ,B be appropriate matrices
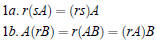 |
Associative and Commutative |
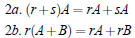 |
Distributive |
1.4 Properties of transpose
Let r ∈ R and A, B be appropriate matrices
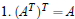 |
Self inverse |
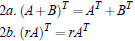 |
Linear |
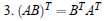 |
2 Special types of Matrices
2.1 Square matrices
Definition. Let A = [aij ] be a square matrix of order n (n× n
type), we say
1. A is a upper triangular matrix if aij = 0 for i > j.
2. A is a lower triangular matrix if aij = 0 for i < j.
3. A is a symmetric if AT = A and skew symmetric if AT
= −A.
4. A is a diagonal matrix if aij = 0 for i ≠ j.
5. A is a scalar matrix if A is diagonal and all elements on the diagonal
are equal to each others, i.e., aij = c for some c ∈R
and for all i = 1,2, . . . ,n.
6. A is an identity matrix if A is scalar and the scalar is 1. We denote
In the identity matrix of order n.
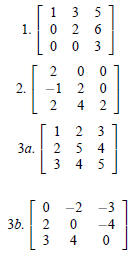
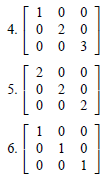
Powers of square matrix
Definition. Let A be a square matrix of order n. Let p be an nonnegative
integer, we define the pth power of A, Ap by

Properties.
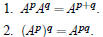
2.2 Nonsingular matrices
Definition. An n× n matrix A is called nonsingular, or
invertible if there exists an n× n matrix B such that
AB = BA = In.
Such B is called an inverse of A, and we write B = A−1. Thus we have
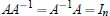
Theorem 1. If A and B are both invertible then AB is also invertible and
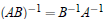
Theorem 2. If A is invertible then A−1 is also invertible and
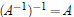
Theorem 3. If A is invertible then AT is also invertible and
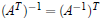
2.3 Linear systems and Inverses
If A is an invertible n× n matrix, then the linear system Ax = b has the unique
solution x = A−1b
Examples. Suppose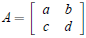 is invertible 1. Prove that
is invertible 1. Prove that
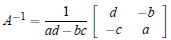
2. Solve the system equation without using methods of elimination
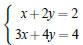
| Prev | Next |