Maximization of Quadratic Functions

I. Introduction.

A. Quadratic functions are among the simplest, and generally most useful, func-
tions that we might hope to encounter.

B. An understandning of their maximization is certainly a good first step in the
direction of understanding maximization of more general functions.

C. It turns out that the theory of quadratic functions is prototypical, in that the
main features are preserved or generalized in the general theory.

II. Quadratic Functions.

A. Polynomials.

1. A polynomial in the variables 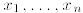is an expression of the form

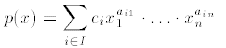
where I is a finite index set and, for each i, 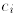is a real number and
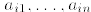are nonnegative integers.

2. Of course polynomials can be added and multiplied . In fact with these
operations the set of polynomials is a commutative ring with unit.

B. Degree

1. The degree of a monomial 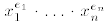is the sum 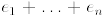of the
exponents , and the degree of the polynomial q above is, by definition, the
maximal degree of any of the monomials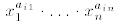

2. A polynomial is said to be homogeneous of degree d if all its monomials
have degree d.

3. Any polynomial p(x) of degree d can be written as a sum



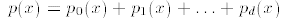
where each 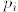is homogeneous of degree i.

4. A quadratic function is a polynomial



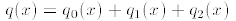
of degree 2.

C. A Matrix Representation

1. The general form of a quadratic function is

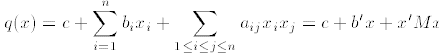
where

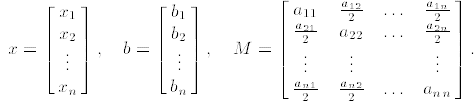
2. An n × n matrix M with entries 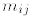is symmetric if it is equal to its
own transpose: 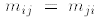for all 1≤ i; j ≤ n. For any quadratic
function as above, there is a unique symmetric matrix representing the
homogeneous part of degree 2. There are other ways of singling out one
particular matrix from the in finite collection that all represent the same
homogeneous polynomial of degree 2. The advantages of the symmetric
representation will emerge as we go along.

D. Differentiation .

1. We define the derivative Dq(x) of q at x to be the function that assigns
to each 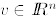the number

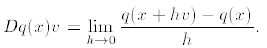
2. We evaluate the difference quotient by computing:

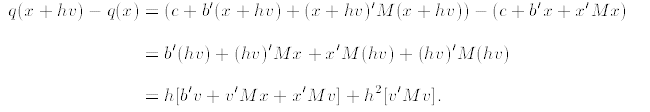
a. The transpose of a 1 ×1 matrix is itself, so
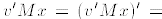
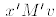, and since M is symmetric we have 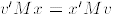. We now
see that



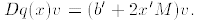
b. Note that Dq(x) is a linear function from IRⁿ to IR.

III. Maximization of Quadratic Functions.

A. The first order condition for maximization states that if 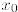is a maximizer of
q(x), then 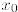is a critical point of q, which means that 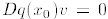for all
.

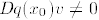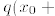
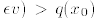1. If   for some v, then we could easily show that either
or 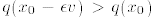for sufficiently small ε, contradicting
the assumption that 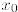is a maximum.

2. If M is invertible, then the only critical point is .

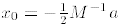3. If M is not invertible, then there are either no critical points or infinitely
many critical points.

B. Assuming that the origin is a critical point, we now want to investigate condi-
tions under which it is a maximum, and when it is the only maximum.

1. The matrix M is positive definite if 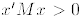for all .
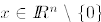2. The matrix M is positive semidefinite if 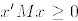for all .
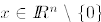3. The matrix M is negative definite if 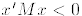for all .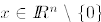
4. The matrix M is negative semidefinite if 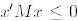for all .

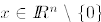C. We now want to characterize symmetric definite matrices. We will show that,
by changing coordinate systems, we can display such a matrix as a diagonal
matrix, with the signs of the entries on the diagonal corresponding to the
version of definiteness being characterized.

IV. Orthogonal Transformations

A. Let P be an n × n matrix, which we think of as representing a change of
coordinates.

1. We ask for the conditions under which P preserves the inner product.

a. The inner product can be represented as a product of matrixes:



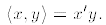
b. For P to preserve the inner product means that for all ,



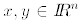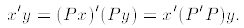
c. This is the case if and only if P'P = I, i.e., .

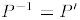2. Such a matrix P is said to be an orthogonal matrix. The set of such
matrices is closed under multiplication and inversion, and is therefore a
group , called the orthogonal group, and typically denoted by O(n).

B. Diagonalization of Symmetric Matrices.

1. If x'Mx is a quadratic form with M a symmetric matrix, it is intuitive
that we would not say that the "geometry" of the function had changed
if we change the coordinates used to represent the point x is a way that
preserved the inner product. Let y denote the same point in the new
system of coordinates , and let the two systems of coordinates be related
by the formula x = Py where P is an n × n orthgonal matrix. We have



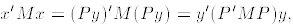
so in the new coordinate system the quadratic form is represented by the
matrix P'MP.

Theorem: If M is a symmetric matrix, there is an orthogonal matrix P such that P'MP
is a diagonal matrix.

Corollary: A symmetric n × n matrix is positive definite (positive semidefinite, nega-
tive definite, negative semidefinite) if and only if, for any orthogonal matrix P such that
P0MP is diagonal, all the diagonal entries of P'MP are positive (nonnegative, negative,
nonpositive).

V. The Characteristic Polynomial.

A. For an n × n matrix M, if Av = λ v for some and some 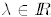, we say
that v is an eigenvector of M while λ is an eigenvalue of M.

1. If λ is an eigenvalue, then M-λI is a singular matrix, and its determinant
is 0.

2. Conversely, if M - λ I is singular, then (M - λI)v = 0 for some v ≠ 0,
and λ is an eigenvalue.

B. The characteristic polynomial of M is the expression

det(M -λ I)

which is a polynomial of degree n.

C. The characteristic polynomial is invariant under coordinate changes: if Q is
any nonsingular matrix, then, since det(AB) = det(A) · det(B) for any n × n
matrices A and B,


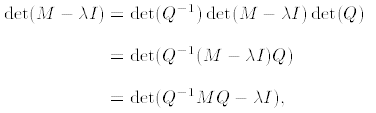
so that M and Q^-1MQ have the same characteristic polynomial.

D. From this we can conclude that, if M is symmetric, all its eigenvalues are real.