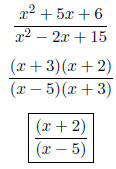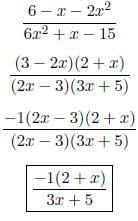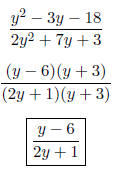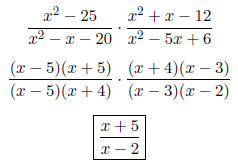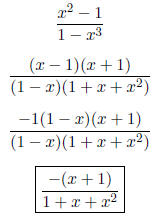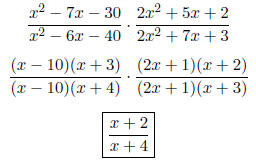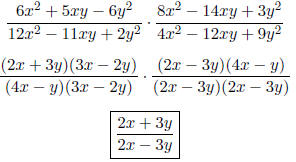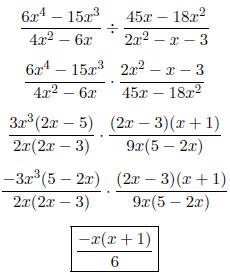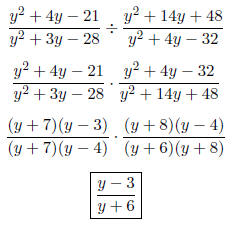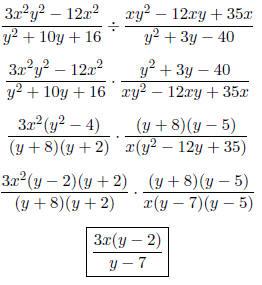MULTIPLICATION AND DIVISION OF RATIONAL EXPRESSIONS
Definitions:
• Rational Expression : is the quotient of two polynomials. For example,
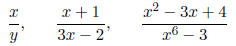
are all rational expressions.
• Lowest terms : A rational expression is in lowest terms when the numerator and
denominator
contain no common factors .
• Reciprocal: The reciprocal of a rational expression a/b is given by b/a
. To find the reciprocal, we invert
(or flip) the rational expression.
Important Properties:
• Fundamental Property of Rational Numbers: If a/b is a rational number and c is any nonzero
real number , then
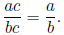
We use this property to write rational expressions in lowest terms.
• To write a rational expression in lowest terms : Factor both the numerator and
denominator
completely. Apply the Fundamental Property of Rational Numbers to eliminate the
common factors.
• To multiply rational expressions: Factor all numerators and denominators as
much as possible.
Apply the Fundamental Property of Rational Numbers to eliminate the common
factors. Multiply
remaining factors.
• To divide rational expressions: Invert the second rational expression and
multiply. In other
words, multiply the first rational expression by the reciprocal of the second .
• If the numerator and denominator of a rational expression are opposites then
the answer is -1. This
is because if we factor out a -1 from either the numerator or denominator, we
have
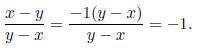
Common Mistakes to Avoid:
• Remember that only common factors can be divided out. For example,
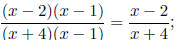 however,
however,
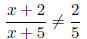 and
and 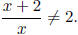
• To multiply (or divide) rational expressions, you do NOT need a common denominator.
• x+y and y +x are NOT opposites of one another. Recall that is does not matter
the order in which
we add terms together. As a result,
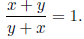
PROBLEMS
Simplify each expression in lowest terms.
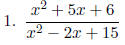
|
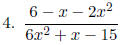
|
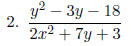
|
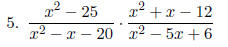
|
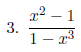
|
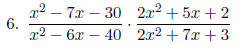
|
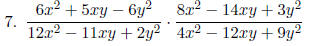
|
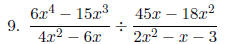
|
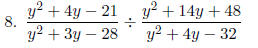
|
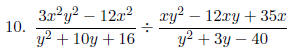
|
| Prev | Next |