On the Nonexistence of Quadratic Lyapunov Function
On the Nonexistence of Quadratic Lyapunov Function
Abstract—We provide an example proving that there
exists no quadratic
Lyapunov function for a certain class of linear agreement /consensus algorithms,
a fact that had been numerically verified in [6].We also briefly discuss
sufficient conditions for the existence of such a Lyapunov function.
Index Terms —Consensus algorithms, Lyapunov theory, multi-agent systems.
I. INTRODUCTION
We examine a class of algorithms that can be used by a
group of
agents (e.g., UAVs, nodes of a communication network, etc.) in order
to reach consensus on a common opinion (represented by a scalar or
vector), starting from different initial opinions, and possibly in the presence
of severe restrictions on inter-agent communications.
We focus on a particular algorithm, whereby, at each time
step , every
agent averages its own opinion with received messages containing the
current opinions of some other agents. While this algorithm is known to
converge under mild conditions, convergence proofs usually rely on the
“span norm” of the vector of opinions. In this note, we address the question
of whether convergence can also be established using a quadratic
Lyapunov function. Among other reasons, this question is of interest
because of its potential implications on convergence time analysis. A
negative answer to this question was provided in [6], where the nonexistence
of a quadratic Lyapunov function was verified numerically. In
this paper, we provide an explicit example and proof of this fact.
In Section II we give some definitions and formally state
the
problem. Section III contains the main result and its proof. Section IV
provides some additional perspective, together with some conditions
under which a quadratic Lyapunov function is guaranteed to exist [1].
II. AGREEMENT ALGORITHM
We consider a set 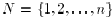 of
agents embedded, at each
of
agents embedded, at each
nonnegative integer time t, in a directed graph
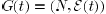 .We
.We
assume that 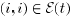 , for all i and t. We define
, for all i and t. We define
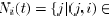
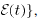 , and let
, and let 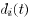 be the cardinality of
be the cardinality of 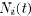 .
.
Each agent i starts with a scalar value
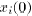 . At each time t, agent i
. At each time t, agent i
receives from every agent 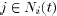 a message with the
value of
a message with the
value of 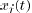 ,
,
and uses the received values to perform the update
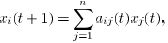
where the 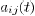 are
nonnegative coefficients that satisfy
are
nonnegative coefficients that satisfy 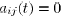 if
if
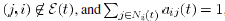 so that
so that 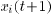 is a weighted
is a weighted
average of the values 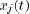 held by the agents at
time t. We define the
held by the agents at
time t. We define the
vector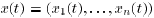 , and note that the algorithm can be
, and note that the algorithm can be
written in the form 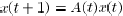 .
.
We next state some conditions under which the agreement
algorithm
is guaranteed to converge.
Assumption 1: There exists some
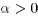 such that if
such that if
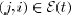 ,
,
then 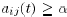 .
.
Assumption 2: (Bounded Intercommunication Intervals):
There
is some B such that for every nonnegative integer k, the graph
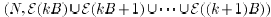 is strongly connected.
is strongly connected.
Theorem 3: Under Assumptions 1–2, and for every
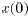 , the components
, the components
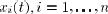 converge to a common limit.
converge to a common limit.
Theorem 3 is presented in [11] and is proved in [10]
(under a slightly
different version of Assumption 2), as well as in [6], for a special case
to be considered below; see also [5], [9] for generalizations and extensions}.
On the other hand, if the graphs 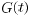 are
symmetric, namely,
are
symmetric, namely,
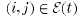 if and only if
if and only if
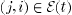 , Assumption 2 can be replaced
, Assumption 2 can be replaced
by the weaker requirement that the graph 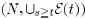 is
strongly
is
strongly
connected for every 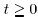 ; see [4], [5], [7],
[9].
; see [4], [5], [7],
[9].
We will focus on a special case, motivated from the model
of Vicsek
et al. [12], and studied in [6], to be referred to as the symmetric,
equalneighbor,
model. In this model, the graphs 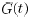 are
symmetric, and
are
symmetric, and
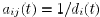 , for every
, for every
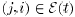 . Thus, each node forms an
. Thus, each node forms an
unweighted average of the values 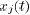 that it has
access to (including
that it has
access to (including
its own).
Theorem 3 is usually proved by showing that the “span
norm”
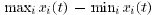 is guaranteed to decrease after a certain
is guaranteed to decrease after a certain
number of iterations . Unfortunately, this proof method usually gives
an overly conservative bound on the convergence time of the algorithm.
Tighter bounds on the convergence time would have to rely on
alternative Lyapunov functions, such as quadratic ones, of the form
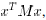 , if they exist.
, if they exist.
Although quadratic Lyapunov functions can always be found
for
linear systems , they may fail to exist when the system is allowed to
switch between a fixed number of linear modes. On the other hand,
there are classes of such switched linear systems that do admit quadratic
Lyapunov functions. See [8] for a broad overview of the literature on
this subject. For the symmetric, equal-neighbor model this issue was
investigated in [6]. The authors write:
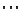 no such common
Lyapunov matrix M exists. While we
no such common
Lyapunov matrix M exists. While we
have not been able to construct a simple analytical example which
demonstrates this, we have been able to determine, for example,
that no common quadratic Lyapunov function exists for the class
of all [ graphs which have] 10 vertices and are connected. One
can verify that this is so by using semidefinite programming
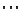
The main contribution of this note is to provide an
analytical example
that proves this fact.
III. THE EXAMPLE
Let us fix a positive integer n. We start by defining a
class Q of
functions with some minimal desired properties of quadratic Lyapunov
functions. Let be the vector in 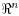 with all
components equal to 1. A
with all
components equal to 1. A
square matrix is said to be stochastic if it is nonnegative and the sum of
the entries in each row is equal to one. Let 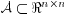 be the set of stochastic
be the set of stochastic
matrices A such that: (i)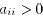 , for all i; (ii)
all positive entries
, for all i; (ii)
all positive entries
on any given row of A are equal; (iii) 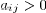 if
and only if
if
and only if 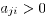 ;
;
(iv) the graph associated with the set of edges
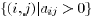 is connected.
is connected.
These are precisely the matrices that correspond to a single iteration
of the equal-neighbor algorithm on symmetric, connected graphs.
Definition 4: A function Q: 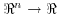 belongs to the
class Q if it
belongs to the
class Q if it
is of the form 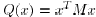 , where:
, where:
a) The matrix 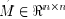 is
nonzero, symmetric, and nonnegative
is
nonzero, symmetric, and nonnegative
definite.
b) For every  , and
, and
 , we have
, we have 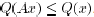 .
.
c) We have 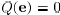 .
.
Note that condition (b) may be rewritten in matrix form as
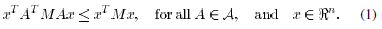
The rationale behind condition (c) is as follows. Let
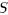 be the subspace
be the subspace
spanned by the vector 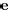 . Since we are
interested in convergence to the
. Since we are
interested in convergence to the
set 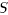 , and every element of
, and every element of
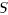 is a fixed point of the algorithm, it is
is a fixed point of the algorithm, it is
natural to require that 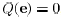 , or, equivalently,
, or, equivalently,
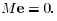
Of course, for a Lyapunov function to be useful,
additional properties
would be desirable. For example we should require some additional
condition that guarantees that 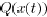 eventually
decreases. However,
eventually
decreases. However,
according to Theorem 5, even the minimal requirements in Definition
4 are sufficient to preclude the existence of a quadratic Lyapunov
function.
Theorem 5: Suppose that 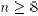 .
Then, the class Q (cf. Definition 4) is empty.
.
Then, the class Q (cf. Definition 4) is empty.
The idea of the proof is as follows. Using the fact the
dynamics of the
system are essentially the same when we rename the components, we
show that if 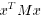 has the desired properties, so
does
has the desired properties, so
does 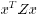 for a matrix
for a matrix
Z that has certain permutation-invariance properties. This leads us
to the conclusion that there is essentially a single candidate Lyapunov
function, for which a counterexample is easy to develop.
Recall that a permutation of n elements is a bijective
mapping 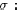
 Let
Let 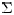 be
the set of all permutations of
be
the set of all permutations of
n elements. For any 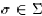 , we define a
corresponding permutation
, we define a
corresponding permutation
matrix 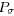 by letting the ith component of
by letting the ith component of
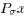 be equal to
be equal to
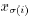 . Note
. Note
that 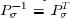 , for all
, for all
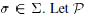 be the set of all permutation
be the set of all permutation
matrices corresponding to permutations in 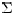 .
.
Lemma 6: Let 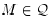 . Define Z
as
. Define Z
as
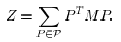
Then, 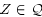 .
.
Proof: For every matrix 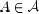 ,
and any
,
and any 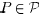 , it is easily seen
, it is easily seen
that 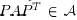 . This is because the transformation
. This is because the transformation
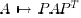
amounts to permuting the rows and columns of A, which is the same
as permuting (renaming) the nodes of the graph.
We claim that if 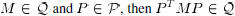 Indeed,
Indeed,
if M is nonzero, symmetric, and nonnegative definite, so is
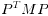 .
.
Furthermore, since 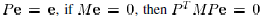 To
To
establish condition (b) in Definition 4, let us introduce the notation
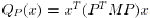 . Fix a vector
. Fix a vector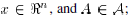 define
define
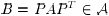 . We have
. We have
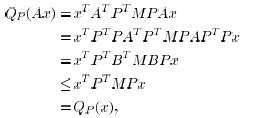
where the inequality follows by applying (1), which is
satisfied by M,
to the vector 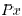 and the matrix B. We conclude
that
and the matrix B. We conclude
that 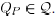
Since the sum of matrices in Q remains in Q, it follows that Z=
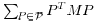 belongs to Q.
belongs to Q.
We define the “sample variance”
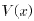 of the values
of the values
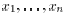 , by
, by
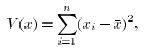
where 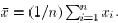 . This is a
nonnegative quadratic function of
. This is a
nonnegative quadratic function of
x, and therefore,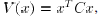 , for a suitable
nonnegative definite,
, for a suitable
nonnegative definite,
nonzero symmetric matrix 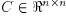 .
.
Lemma 7: There exists some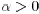 such
that
such
that
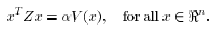
Proof: We observe that the matrix Z satisfies
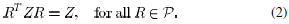
To see this, fix R and notice that the mapping
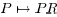 is a bijection
is a bijection
of  onto itself, and therefore,
onto itself, and therefore,
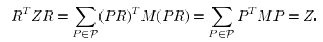
We will now show that condition (2) determines Z, up to a
multiplicative
factor . Let 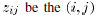 th entry of Z. Let
th entry of Z. Let
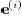 be the
be the
ith unit vector, so that 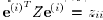 . Let
. Let
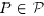 be a permutation
be a permutation
matrix that satisfies 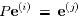 . Then,
. Then,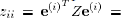
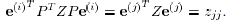 Therefore, all diagonal entries
Therefore, all diagonal entries
of Z have a common value, to be denoted by z.
Let us now fix three distinct indices
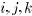 , and let
, and let
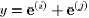 ,
,
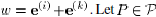 . Let be a permutation matrix such that
. Let be a permutation matrix such that
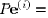
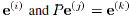 , so that
, so that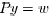 . We have
. We have
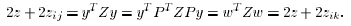
By repeating this argument for different choices of
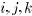 , it follows
, it follows
that all off-diagonal entries of Z have a common value to be denoted
by r. Using also the property that 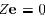 , we
obtain that
, we
obtain that 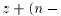
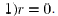
This shows that the matrix Z is uniquely determined, up to a
multiplicative factor .
We now observe that permuting the components of a vector x
does
not change the value of 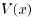 . Therefore,
. Therefore,
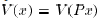 for every
for every
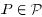 , which implies that
, which implies that
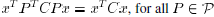 and
and
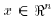 . Thus, C satisfies (2). Since all matrices
that satisfy (3) are
. Thus, C satisfies (2). Since all matrices
that satisfy (3) are
scalar multiples of each other, the desired result follows.
Proof of Theorem 5: In view of Lemmas 6 and 7, if Q is
nonempty, then 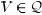 . Thus, it suffices to show
that
. Thus, it suffices to show
that 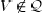 . Suppose
. Suppose
that 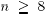 , and consider the vector x with
components
, and consider the vector x with
components 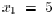 ,
,
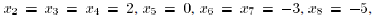 and
and
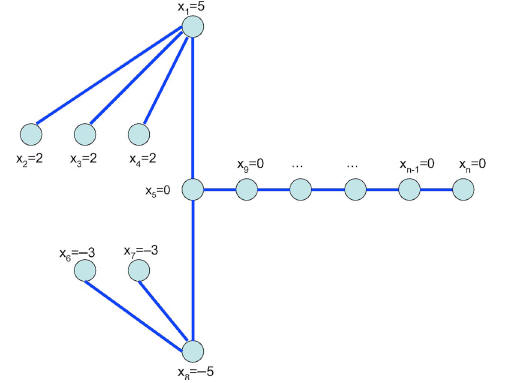
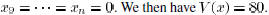 Consider the outcome
Consider the outcome
of one iteration of the symmetric, equal-neighbor algorithm, if the
graph has the form shown in Fig. 1. After the iteration, we obtain the
vector y with components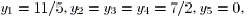
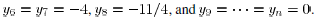 We have
We have
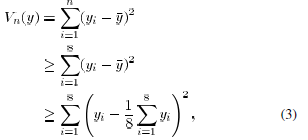
where we used that 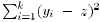 is
minimized when
is
minimized when 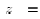
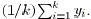 . A simple calculation shows that the
expression (3)
. A simple calculation shows that the
expression (3)
evaluates to 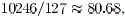 , which implies that
, which implies that
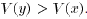 .
.
Thus, if 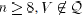 and the set Q is empty.
and the set Q is empty.
IV. CONDITIONS FOR THE EXISTENCE OF A QUADRATIC LYAPUNOV FUNCTION
Are there some additional conditions (e.g., restricting
the matrices
A to a set smaller than 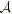 ), under which a
quadratic Lyapunov function
), under which a
quadratic Lyapunov function
is guaranteed to exist? We start by showing that the answer is positive
for the case of a fixed matrix (that is, if the graph
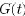 is the same for
is the same for
all t).
Let A be a stochastic matrix, and suppose that there
exists a positive
vector 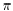 such that
such that
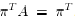 . Without loss of generality, we can
. Without loss of generality, we can
assume that 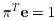 . It is known that in this case,
. It is known that in this case,
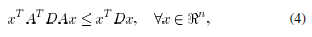
where D is a diagonal matrix, whose th diagonal entry is
equal to 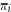
(cf. Lemma 6.4 in [2]). However,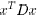 cannot be
used as a Lyapunov
cannot be
used as a Lyapunov
function because 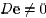 (cf. condition (c) in
Definition 4). To remedy
(cf. condition (c) in
Definition 4). To remedy
this, we argue as in [3] and define the matrix
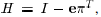 , and
, and
consider the choice 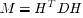 . Note that M has rank
. Note that M has rank
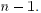 .
.
We have 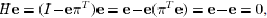 , as desired.
, as desired.
Furthermore,
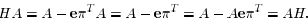
Using this property, we obtain, for every
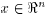 ,
,
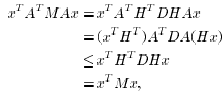
where the inequality was obtained from (4), applied to
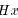 . This shows
. This shows
that 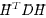 has the desired properties (a)–(c) of
Definition 4, provided
has the desired properties (a)–(c) of
Definition 4, provided
that 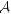 is replaced with
is replaced with
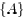 .
.
We have just shown that every stochastic matrix (with a
positive left
eigenvector associated to the eigenvalue 1) is guaranteed to admit a
quadratic Lyapunov function, in the sense of Definition 4. Moreover,
our discussion implies that there are some classes of stochastic matrices
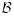 for which the same Lyapunov function can be
used for all matrices
for which the same Lyapunov function can be
used for all matrices
in the class.
a) Let 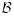 be a set of
stochastic matrices. Suppose that there exists a
be a set of
stochastic matrices. Suppose that there exists a
positive vector such that 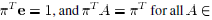
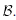
Then, there exists a nonzero, symmetric, nonnegative definite
matrix M, of rank 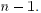 , such that
, such that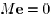 , and
, and 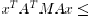
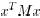 , for all x and
, for all x and
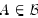
b) The condition in (a) above is automatically true if all
the matrices
in 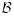 are doubly stochastic (recall that a
matrix A is doubly stochastic
are doubly stochastic (recall that a
matrix A is doubly stochastic
if both A and 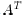 are stochastic); in that
case, we can take
are stochastic); in that
case, we can take 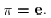
c) The condition in (a) above holds if and only if there
exists a
positive vector 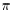 , such that
, such that
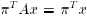 , for all
, for all
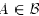 and
and
all x. In words, there must be a positive linear functional of the
agents’ opinions which is conserved at each iteration. For the
case of doubly stochastic matrices, this linear functional is any
positive multiple of the sum 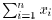 of the agents’
values (e.g.,
of the agents’
values (e.g.,
the average of these values).
ACKNOWLEDGMENT
The authors are grateful to Ali Jadbabaie for useful
discussions about
this problem.
| Prev | Next |