Other Types of Equations
Equations with Radical and Rational Exponents
When solving an equation linear in form with radicals or
rational exponents , simplify the equation , isolate the most
complicated radical on one side, and raise both sides to
the power equal to the index of the radical in order to
eliminate the last. You may need to repeat this procedure
if the resulting equation still contains a radical.
Note: We solve radical equations over the real numbers .
Caution! If you raise both sides of an equation to
an
even power, the new equation may have more real
solutions than the original one.
Example: Equation x = 6 has solution set: {6}.
Raising both sides to the power 2, gives the equation
x^2 = 36 which has solution set x = ±6.
Thus, x = −6 is an extraneous solution to the original
equation and must be rejected.
Important! When raising to an even power, always
check each proposed solution in the original equation.
Example: Solve
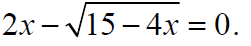
Example: Solve
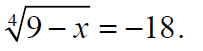
Note: If n is an even number,
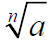 is never negative .
is never negative .
Example: Solve the equation
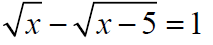
Example: Solve the equation
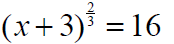
Equations Quadratic in Form
Example: Solve by using a substitution.
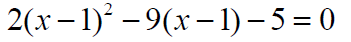
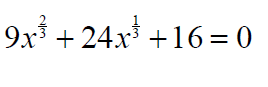
Equations Quadratic in x^2 (Biquadratic)
Example:
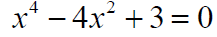
Solve the equation in the complex number system
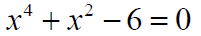
Factorable Equations
Example: Find all solutions of the equation:
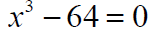
Example: Solve by factoring
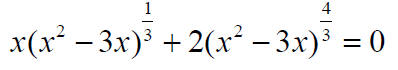
Equations with Absolute Value
Recall:
1.|x| is the distance on the number line from 0 to x.
2.|x|≥ 0
3.|x|= 0 if and only if x = 0
4.|x|= −x
5. The algebraic definition :
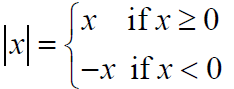
If a is a positive real number and u is any algebraic
expression , then
|u|= a is equivalent to u = a or u = −a .
Example: Solve the equations.
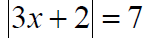
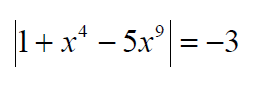
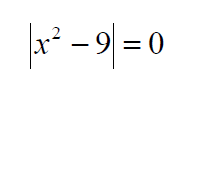
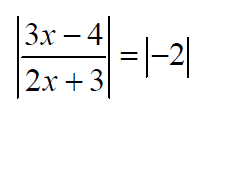
| Prev | Next |