Polynomial Codes and some lore about Polynomials

10.1 Introduction:

We will now introduce more structure for our message words and code words,
and use it to get single error correcting codes that can be described more easily, as well as
codes that can correct several errors.

We do this by treating our sequences as polynomials and defining
multiplication for them .

Given a sequence, say 1011, we can make it into a polynomial by converting each
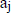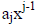bit into and adding the results , For the sequence 1011 we get 1 + x² + x³.

We multiply our sequences by the usual laws of multiplication, again with the
2=0 rule Thus, in multiplying (111) by (1011). We multiply 1+x+x² by 1+x²+x³ which
using the distributive law comes to 1 + x +2x²+ 2x³ + 2x⁴ + x⁵ which we interpret to be
1 +x+x⁵.

We will describe encoding by use of an encoding polynomial p(x) and our rule for
encoding will be



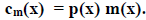
Thus the task of finding useful codes is, in this context, the task of finding useful
polynomials. In order to find them we first look at some properties of polynomials.

10.2 Binary Polynomials

We will find, that if you want to find efficient single error correcting polynomial
codes, you can do so by choosing an encoding polynomial that is "primitive". Primitive
means prime, plus one other property we shall soon describe. So we will begin by
looking at low degree prime polynomials.

Recall that binary numbers obey these rules for addition:

0 + 0 = 1+1 = 0
1 + 0 = 0+1 = 1

and these for multiplication:

0*0 = 0*1 = 1*0 = 0
1*1 = 1.

A polynomial defined over this "field" (the field is called GF(2)) is no more
than a polynomial whose coefficients are each 0 or 1.

Here is a polynomial of degree 5: 1 + x² + x⁵.

Polynomials have the wonderful property that you can add and subtract them and
also multiply and divide them using all the standard commutative, distributive and
associative laws of arithmetic.

When you divide one polynomial by another, you get a quotient polynomial, and
perhaps a remainder. The rules for dividing are the rules for long division. (actually,
when you write a number as say 543 you are treating it as a sort of polynomial, namely
5*10² + 4*10 + 3, with 10 instead of a variable, so the rules for dividing same are the
rules for polynomials, except for carrying, which you do with numbers and not with
polynomials. (in our case, given 2=0, there is no carrying to do)

With our polynomials life is much more pleasant than what you encountered in
your youth when you want to do arithmetic since the only possible non- zero coefficient
of our polynomials is 1,

We give an illustration of division of polynomials.

Suppose we want to divide x⁸ by 1 + x² + x⁵.

The latter goes x³ times into the former, with a remainder of x⁵ + x³. It goes once into this
remainder with x³ + x² + 1 left over. The resultant quotient is therefore x³ + 1 with
remainder x³ + x² + 1..

A polynomial is said to be prime if it cannot be factored into polynomials of
lower degree.

The polynomial of degree 5 above happens to be prime. On the other hand the
polynomial (1 + x² + x⁴) is not prime, being (1 + x + x²)².

We will now look at polynomials of low degree and identify which are primes.

We can immediately see that x is the only monomial that is prime ; the rest have it
as a factor.

Any polynomial, p(x) with an even number of terms has (1 + x) as a factor.

Why?

Because if you set x = 1 you find p(1)=0, when p has an even number of terms.

When you divide p(x) by (1+x) you get a remainder that must have 0 degree and
so must be 0 or 1.

But we have p(x)=q(x)(1+x) + r(x) with q(x) the quotient upon dividing p by (1+x), and
r(x) the remainder.

Evaluating this at x=1 we get 0 = p(1) = q(1)*0 + r(1) .

From which we conclude that r=r(1) = 0, and this means (1+x) divides any polynomial
with an even number of terms

Any polynomial without a 1 term is divisible by x.

Further, any polynomial whose terms all have even degree is the square of
the polynomial whose degrees are all half of its, so it cannot be prime.

This is true because the ugly cross terms which normally occur when you square a
polynomial all have factors of 2 multiplying them so they are all 0 here.

There is one more fact that is useful when examining polynomials.

If we take a sequence like 1011 and make it into a polynomial, we can do so in two ways.

The way we have chosen is to start from the left, and have successive bits correspond to
increasing powers .

We could just as well have done the same thing starting from the right.

But this gives us a different polynomial , which we call the "reverse polynomial" to the
first.

In our example, our polynomial is 1 +x² + x³ and the reverse one is 1+x+x².

Now no important property of our code can depend on whether we started from the left or
the right in turning our sequences into polynomials.

We conclude from this that the properties of a polynomial and its reverse such as
primitivity and primeness must be the same for each polynomial and its reverse.
This conclusion will be justified by what we see very soon: that these properties have a
direct effect on the error correcting properties of the code a polynomial generates.

So let us explore the polynomials of low degree and classify them as prime or
composite.

There are two polynomials of degree 1, x and 1+x and both are prime
:
The only polynomial of degree 2 with terms 1 and x² and an odd number of terms
is 1 + x + x², and therefore it is the only possible prime. It is prime, as you can see
because it is not a product of any combination of the degree 1 primes. It is symmetric on
reversal of bits

The only possible primes of degree three with odd number of terms having 1 and
x³ as terms are 1 + x + x³ and 1+ x² + x³ which are reverses of one another. If they were
not primes they would have to have a factor of degree 1, but they do not, because they
have an odd number of terms.

Among polynomials of degree 4 the only polynomials with an odd number of
terms not all squares with a constant term and one of degree 4 are 1 + x + x⁴, 1 + x³ + x⁴,
which are reverses of one another and 1+x+x²+x³+x⁴. which is symmetric. By the
reasoning used for polynomials of degree 3 in the last paragraph, all of these are prime.
(The square of (1+x+x²) is 1+x²+x⁴)

By similar reasoning the candidates for primes of degree 5 are 1+ x+ x⁵, 1+x² +
x⁵, all terms except x, all terms except x² and the reverses of these 4 polynomials
Of these (1+x+x²)(1+x+x³) and its reverse are not prime and the others are prime.

You could, if you wanted to, continue this investigation to degree 6,…,10 at least .
For example, for degree 8, by my calculation, there are 64 polynomials with an odd
number of terms including 1 and x⁸, which form 28 pairs of a polynomial and its reverse,
and 8 symmetric polynomials. Of these about half are primes.