polynomials denominators
Multiplifying polynomials
Recall that in general (a+b)2 ≠ a2+b2
Example 0.1 let a = 3 and b = 4
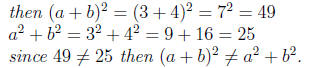
Using the distributive property and the FOIL property we
can multiply rad -
ical expressions in the same way we multiplied polynomials.
Example 0.2
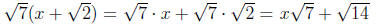
Example 0.3
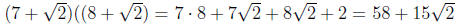
Example 0.4
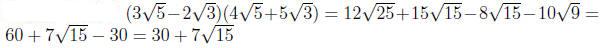
Example 0.5
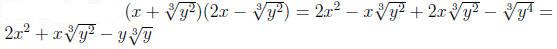
We do not want to leave roots in the denominator of a
fraction. When we
encounter a single root in the denominator just multiply the top and bottom
of the fraction by a value that will create an integer in the denominator.
Example 0.6
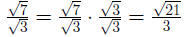
Example 0.7
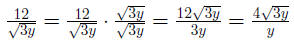
Example 0.8
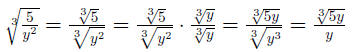
Definition 0.1 The conjugate of a + b is a - b.
When the denominator contain two terms , we rationalize the denominator
by multiplying the top and bottom of the fraction by the conjugate of de-
nominator.
Example 0.9
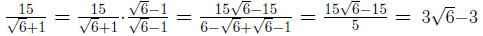
Example 0.10
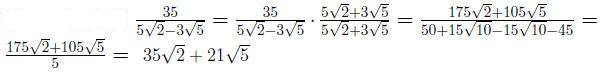
Example 0.11
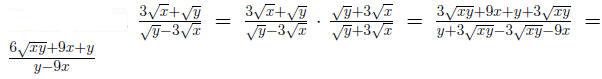
| Prev | Next |