Properties of Exponents I

A. Product Rule

Notice the following:

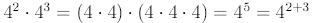
Similarly,

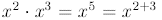
In general,

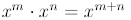
Thus, when we multiply powers , we add exponents .

Example:

Find

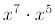
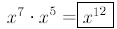(by adding exponents )

B. Quotient Rule

Notice the following:

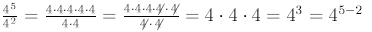
Similarly,

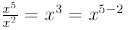
In general,

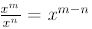
Thus, when we divide powers , we subtract exponents .

Example:
Find

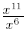
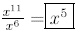(by subtracting exponents)

C. Power Rule

Notice the following:

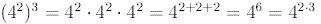
Similarly,

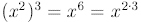
In general,

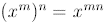
Thus, when we take a power of a power, we multiply exponents.

Example:

Find

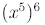
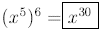(by multiplying exponents)

WARNING: Don’t get the product and power rules confused:

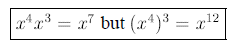
D. Zero Power

Notice the following: 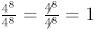, but by the quotient rule,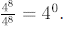

Thus, we see that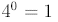

Similarly,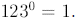

The above argument works for any number , except zero, because we would have 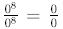which is indeterminate.

In general,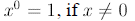

E. Negative Exponents

Notice the following:

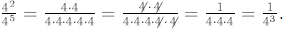
However 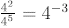by the quotient rule.

Thus,

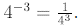
Similarly,

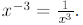
In general,

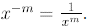
Thus, a negative exponent means reciprocal.

Example:
Find

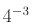
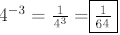(negative exponent rule )

F. Switch Rule

By using the reciprocal idea for negative exponents, we get the switch rule:

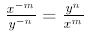
Thus, in a fraction , powers in the top get sent to the bottom by negative exponents, and
powers in the bottom get sent to the top by negative exponents.

Example:
Rewrite without negative exponents:

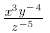
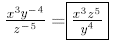(using the switch rule)

G. Multiple Power Rule

By using the power rule idea , we see that if we have a fraction to a power, we hit every
entry with the power (and multiply exponents).

Thus,

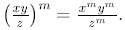
Example:
Find

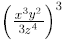
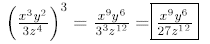
H. Comments on Rules

1. It is important to memorize these rules, and to not get them confused.

2. Parentheses are important !:

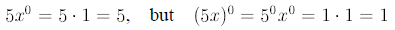
3. If everything “leaves” a numerator or denominator , you leave “1” behind:

For example:

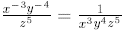
4. With fractions, variables not in a fraction are considered to be in the numerator.

For example:

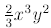
is the same as

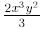
5. When using the quotient rule:

If you use it on a variable, the answer goes in the numerator. If you don’t use it, the
variable stays put.

For example:

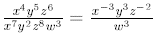
In this example,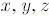 are put in the numerator, and w stays put.

6. When using the multiple power rule:

It is only correct to use it if the variables are not added or subtracted:

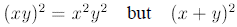can’t be simplified by this rule .

We will explain how to simplify 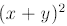later in the course. For the time being,
remember the rule:

DON’T APPLY POWERS ACROSS PLUS OR MINUS SIGNS