Rational Expressions and Equations

In this section we want to conclude our review of the ideas we need from elementary algebra . Other important topics to review will be included later.

Here we want to review rational expressions . Recall a rational expression is just any fraction that contains a polynomial. This includes all fractions with or without variables.

We want to start by simply reducing rational expressions. This merely requires factoring and canceling any common factors.

Example 1:

Simplify.

Solution:
a. To simplify this rational expression we simply need to reduce the number part and cancel any variables that we can . We get

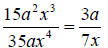
b. This time we need to factor the numerator and denominator completely first. Then we cancel any common factors. This gives us

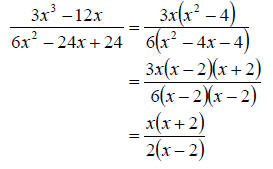
Next we want to perform all the basic operations on rational expressions, that is, adding, subtraction, multiplying and dividing rational expressions.

Recall that the techniques that we use in order to do this are the same techniques we used for regular fractions. That is, to add and subtract , we need to have the LCD. To multiply we simply multiply straight across (we actually factor and cancel first) and for dividing we invert the second fraction and then multiply.

Example 2:

Perform the operations.

Solution:
a. To multiply we need only factor all numerators and denominator and cancel any common factors. We get

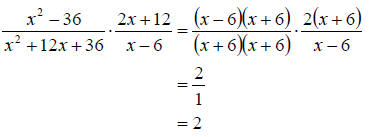
b. For division, we need to invert the second fraction (i.e. flip it upside down), then multiply as usual by factoring and canceling. We get

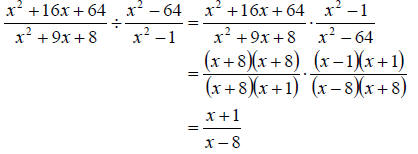
c. To add rational expression we will need to find the LCD. So first we should factor all denominators. This gives

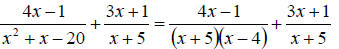
Clearly the LCD is 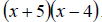We need each denominator to have the LCD so we can add the numerators. To accomplish this, we need to multiply the numerator and denominator by whatever it takes to get each fraction to have the LCD. Clearly the first fraction needs nothing. However, the second fraction needs an x – 4. So we once we do this we can just add the numerators and reduce. We proceed as follows

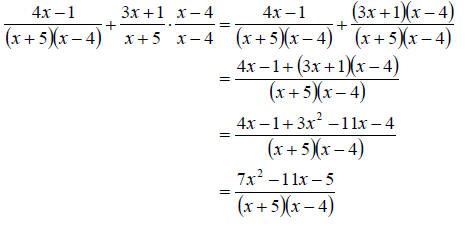
d. Similarly, we can see the LCD here is 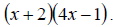So we multiply each fraction on numerator and denominator by what it is missing from the LCD. We then subtract numerators and simplify. We get

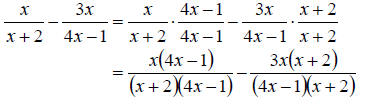
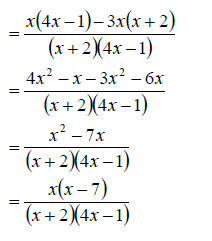
Also, when dealing with rational expressions, sometimes we have to deal with fractions inside fractions. We call these complex (or compound) fractions. We simplify them by multiplying numerator and denominator by the LCD of all the fractions in the expression.

Example 3:

Simplify.

Solution:
a. To simplify this expression, we will multiply numerator and denominator by the LCD of all the fraction contained in the expression. That is, x^2 here. Then we reduce and simplify. We get

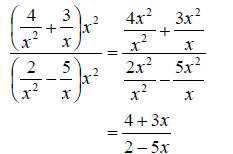
So since the rational expression is fully reduced, we are finished.

b. This time the LCD is 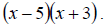So multiplying on numerator and denominator gives us

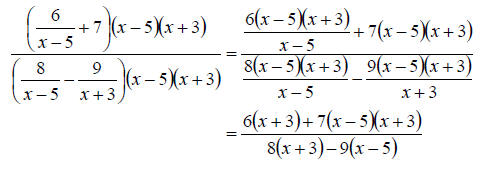
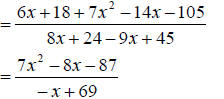
Next we want to remember how to solve an equation that contains a rational expression and also how to solve equations that contain more than one variable, called a literal equation.

To solve rational equations we simply multiply both sides of the equation by the LCD. This will “clear” the fractions. We must, though, remember to check our answers, since we cannot ever have a denominator equal to zero . If one of our values makes the original equation have a denominator of zero, we must omit it and only keep those solutions that check .

To solve literal equations , we just use the same techniques we did before for solving equations. Its just that now we end up with an expression for a solution, not just a number.