Reduce All Fractions to Lowest Terms
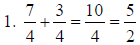 |
1. 5/2 |
Keep the common denominator , add the
numerators, reduce.
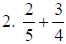 |
2. 23/20 |
a. Use common denominator of 20.
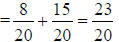
b. use “the formula”
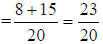
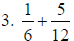 |
3. 7/12 |
Use common denominator of 12
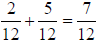
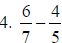 |
4. 2/35 |
a. Use C.D. of 35
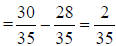
b. Use the formula
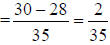
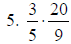 |
5. 4/3 |
a. Multiply numerators , multiply denominators;
reduce
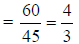
b. reduce first
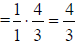
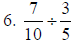 |
6. 7/6 |
Invert and multiply
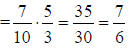
You could also reduce before you multiply
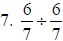 |
7. 1 |
Invert and multiply
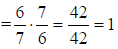
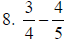 |
8. -1/20 |
Using the formula:
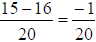
B. Numbers
1. Define “ rational number ” A fraction; a number
that can be written as the ratio of two integers.
It will be a terminating or repeating decimal.
2. Circle the integers : 2, -2, 0
Integers are not fractions , but they can be positive
or negative.
| 3. -|-8| = -(8) | 3. -8 |
Circle T or F
| 4. |12| = |-12| | 4. T |
| 5. -(-8) = 8 | 5. T |
| 6. -5 < -4 | 6. T |
| 7. |-5| ≥ |-4| | 7. T |
| 8. 4 ≤ 4 | 8. T |
C. Perform the indicated operations
| 1. 2 - (-6) = 2 + 6 | 1. 8 |
| 2. -4 + 7. Start at -4, go 7 steps right . | 2. 3 |
| 3. -7 - (-10) = -7 + 10 | 3. 3 |
| 4. -6 - 3. Start at -6; go 3 steps left. | 4. -9 |
| 5. 7 + (-5) = 7-5 | 5. 2 |
| 6. (4)(3) | 6. 12 |
| 7. (4)(-3) | 7. -12 |
| 8. (-4)(-3) | 8. 12 |
| 9. -12 ÷ (-4) = -12·(-1/4)> multiplying two negatives gives a positive |
9. 3 |
| 10. -2/3 ÷ (1/3) = -2/3·(3/1) | 10. -2 |
D. Use the order of Operations
| 1. 3 + 2·4 = 3 + 8 | 1. 11 |
| 2. 12 - 3(4 - 1) = 12 - 3(3) = 12 - 9 |
2. 3 |
| 3. 1 + 3[17 - 3(2 + 3)] = 1+ 3[17 - 3(5)] = 1+ 3[17 - 15] = 1+ 3[2] = 1+ 6 |
3. 7 |
| 4. 4 (7 - 5) = 4(2) |
4. 8 |
E. Simplify each expression. Write “CBS” if it cannot be simplified
| 1. 4n + 8x + 5x + 3n Combine like terms |
1. 7n + 13x |
| 2. 3ab + 4a. Unlike terms | 2. CBS |
| 3. 4a + 3b - 5 + 2(a + 2b + 1) remove brackets =4a + 3b - 5 + 2a + 4b + 2 combine like terms |
3. 6a + 7b - 3 |
| 4. 5x + 3x2 Unlike terms | 4. CBS |
F. Properties
1. Which property says that a + b = b + a
1.
commutative
2. Which property says that (ab)c = a(bc)
2. associative
3. use the distributive property to rewrite: -3(- 4y + 5)
3. 12y - 15
G. Rewrite each equation by: removing fractions,
decimals and brackets and combining like terms
You need not solve
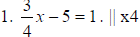 3x - 20 = 4 |
1. 3x - 20 = 4 |
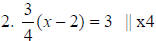 3(x - 2) = 12 || distribute bracket 3x - 6 = 12 || +6 |
2. 3x - 6 = 12 |
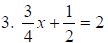 Multiply x 4 3x + 2 = 8 |
3. 3x + 2 = 8 |
| 4. .4x + 4.2 = 5 Move all decimals one place 4x + 42 = 50 |
4. 4x + 42 = 50 |
| 5. .3 + .04x = .42 Move all decimals two places 30 + 4x = 42 |
5. 30 + 4x = 42 |
H. Linear Equations. Solve each of the following for x
| 1. x - 8 = 12 add 8 to both sides |
1. x = 20 |
| 2. x - 2 = -7 add 2 to both sides |
2. x = -5 |
| 3. 5x -5 = 20 add 5 to both sides 5x = 25 divide by 5 |
3. x = 5 |
| 4. -3x = -12
divide by -3. |
4. x = 4 |
| 5. -6x + 5 = 29 subtract 5 -6x = 24 divide by -6 x = -4 |
5. x = -4 |
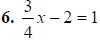 multiply by 4 3x - 8 = 4. add 8 3x = 12. divide by 3 x = 4 |
6. x= 4 |
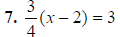
Multiply by 4 |
7. x = 6 |
| 8. 8x - 4 = 5x + 11 subtract 5x 3x - 4 = 11. add 4 3x = 15. divide by 3 x = 5 |
8. x = 5 |
| 9. 5x – 4 = 8x - 16 subtract 5x -4 = 3x -16. add 16 12 = 3x. Divide by 3 4 = x |
9. x = 4 |
| 10. -.7x + 5 = .3x + 2 multiply by 10 (move all decimals one place) -7x + 50 = 3x + 20. add 7x 50 = 10x + 20. subtract 20 30 = 10x divide by 10 3 = x |
10. x = 3 |
I. Inequalities. Solve and Graph
1. 4 + 3x ≥ 11 1. x≥ 7/3
3x ≥ 7
x ≥ 7/3

2. 2 - 4x > 14 2. x < -3
-4x > 12. Divide negative 4. Reverse the inequality
x < -3
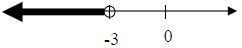
3. 0 < 4x + 12  ≤ 20
3. -3 < x ≤ 2
≤ 20
3. -3 < x ≤ 2
subtract 12 from all three parts
-12 < 4x ≤ 8. Divide by 4
-3 < x ≤2
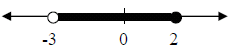
| Prev | Next |