REVIEW OF FUNDAMENTALS
R.5 Circles and Parabolas
PREREQUISITES
1. There are no prerequisites for this section other than some high school
analytic geometry; however, if the material presented in this section
is new to you, it would be a good idea to enroll in a precalculus course.
This section is intended to be a review.
GOALS
1. Be able to recognize equations for circles and parabolas, and be able
to describe their graphs.
2. Be able to solve simultaneous equations to find intersection points.
STUDY HINTS
1. Circles. The general equation is (x - a)2 + (y - b)2 = r2 , where
(a,b) is the center of the circle and r is the radius. Any equation
of the form Ax2 + Ay2 + Bx + Cy + D = 0 may be written in the general
form of a circle by completing the square. If r2 > 0 , then the
equation describes a circle. The coefficient of x2 and y2 must be
the same.
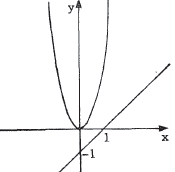
2. Parabolas. The general equation is y - q = a(x - p)2 , where (p,q)
is the vertex. The parabola opens upward if a > 0 , downward if
a < 0 . The graphs of all quadratic equations of the form y = ax2 +
bx + c are parabolas.
3. Simultaneous equations. The solutions represent points of intersection.
One method of solution is to multiply equations by a constant factor and
then subtract equations to eliminate a variable as in Example 6 . The
other method uses substitution to eliminate a variable as in Example 7.
SOLUTIONS TO EVERY OTHER ODD EXERCISE
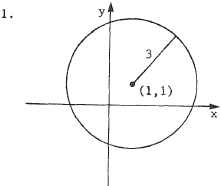 |
A circle with center at (a,b) and radius r has the equation (x - a)2 + (y - b)2 = r2 . With center (1,1) and radius 3 , the equation is (x - 1)2 + (y - 1)2 = 9 or x2 - 2x + y2 - 2y = 7 . |
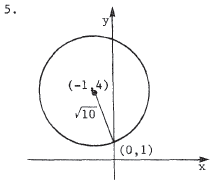 |
A circle with center at (a,b) and radius r has the equation (x - a)2 + (y - b)2 = r2 . With center at (-1,4) , the equation is (x +1)2 + (y - 4)2 = r2 . Substituting in (0,1) yields 12 + (-3)2 = r2 = 10, so the desired equation is (x + 1)2 + ( y - 4 ) 2 = 10 or x2 + 2 x + y2 - 8 y + 7 = O . |
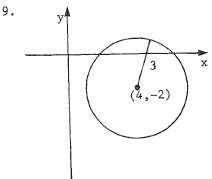 |
We complete the square to find the center and radius. -x2 - y 2 + 8 x - 4 y - 1 1 = 0 is equivalent to x 2 + y2 - 8x + 4y + 11 = 0 , i.e., (x2 - 8x + 16) + (y2 + 4y + 4) = -11 + 16 + 4 = 9 = (X - 4)2 + (y + 2)2 . Thus, the center is (4,-2) and the radius is 3 . |
The parabola with vertex at (p,q) has the general equation
y - q =
a(x - p)2 . In this case, y - 5 = a(x - 5)2 . Substituting (0,0)
yields -5 = a(-5)2 , so a = -1/5 and the equation becomes y =
-(x - 5)2/5 + 5 = -x2 /5 + 2x .
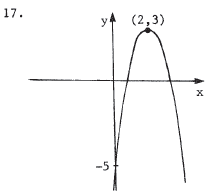 |
We complete the square to get the form y - q = a(x - p)2 , where (p,q) is the vertex. y = -2x2 + 8x - 5 implies (y + 5) - 8 = -2(x2 - 4x + 4) = -2(x - 2)2 = y - 3 . Thus, the vertex is (2,3) and since a = -2 < 0 , the parabola opens downward. |
 |
y
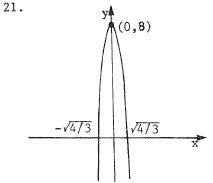
= -6x2 + 8 is the same as y - 8 = -6 (x - 0 ) 2. This has the form y - q = a(x - p) 2 , so the vertex is (p ,q) or (0,8) . Since a = -6 < 0 , the parabola opens downward. |
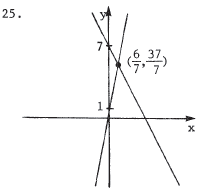 |
To find the point of intersection, solve the equations simultaneously. -2x + 7 = y = 5x + 1 implies 6 = 7x , i.e., x = 6/7 . Substituting back into one of the equations, we get y = 5(6/7) + 1 = 37/7 , so the point of intersection is (6/7,37/7) . To graph the equations, we see that |
y = -2x + 7 is a line with slope -2 and y- intercept 7. y = 5x + 1 has
slope 5 and y-intercept 1.
|
29.
|
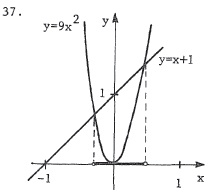
To find the point of intersection
, solve the equations simultaneously. Thus, y - x + 1 = 0 becomes 3x2 - x + 1 = 0 . The quadratic formula yields 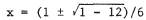 . Therefore, . Therefore,the parabola and the line do not intersect. To graph the equations, we see that |
y = 3x2 is an upward opening parabola with vertex at (0,0) . y -
x +
1 = 0 is equivalent to y = x - 1 , which is a line with slope 1 and
y-intercept -1 .
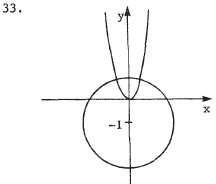 |
We solve the equations simultaneously. y = 4x2 becomes y/4 = x2 , so x2 + 2y + y2 - 3 = 0 = y / 4 + 2 y + y2 - 3 = y2 + 9 y / 4 - 3 . By the quadratic formula , 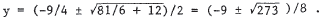 From y = 4x2 , we have 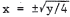 , and , andy must be non- negative . Thus, the inter - |
section points are 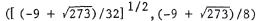 and
and
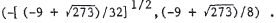
y = 4x2 is a parabola opening upward with vertex at the origin .
x2 + 2y +y2- 3 = 0 is equivalent to x2 + (y2
+ 2y + 1) = 4 or x2 +
(y + 1)2 = 22 . This is a circle centered a t (0,-1) with radius 2 .
 |
9x2 < x + 1 implies 9x2 - x - 1 < 0 . The solution of 9x2 - x - 1 = 0 is 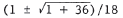 . 1/18 satisfies . 1/18 satisfies9x2 < x + 1 , and since 1/18 lies between the solutions of 9x2 - x - 1 = 0 , the solution of the inequality is 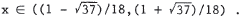 |
Geometrically, the solution intervalis where the line x + 1 lies
above the parabola 9x2 .
SECTION QUIZ
1. The curves y - 1 = x4 and y = 2x2 intersectat two points. Find
them.
2. They c a l l e d h e r Melody the Marcher because she always got her
employees
t o march off t o work. After working a day for the Marcher, you no longer
needed to be t o l d , "Get t o work!" Her glaring eyes told you, "You better
march back t o work!" She wanted a circular fence of radius 7 t o protect
a prized t r e e a t (2,3) . One of the hire d hands came up with a devious
plan. He decided to make a parabolic fence passing through (9,3),(-5,3)
and ( 2 , - 4 ) . After the fence was half finished , he asked her t o
stand a t
the focus (see Fig. R.5.4). When the Marcher arrived, the other employees
threw garbage a t the wall to r e f l e c t back a t the focus.
(a) What is the equation of the parabola?
(b) What is the equation of the circle ?
( c ) Sketch both curves on the same s e t of axes.
ANSWERS TO SECTION QUIZ
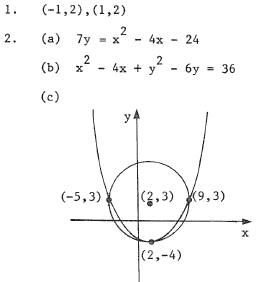
| Prev | Next |