Solution of Quadratic Equations
After reading this chapter, you should be able to:
1.find the solutions of quadratic equations,
2.derive the formula for the solution of quadratic equations,
3. solve simple physical problems involving quadratic equations.
What are quadratic equations and how do we solve them?
A quadratic equation has the form
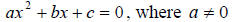
The solution to the above quadratic equation is given by
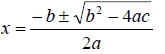
So the equation has two roots , and depending on the value of the discriminant
,
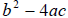, the equation may have real , complex or
repeated roots.
If
,
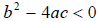the roots are complex .
If
,
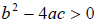the roots are real .
If
,
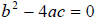the roots are real and repeated.
Example 1
Derive the solution to
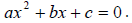
Solution
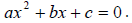
Dividing both sides by a,
,
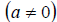we get
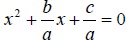
Note if a=0, the solution to
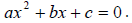
is
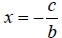
Rewrite
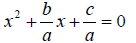
as
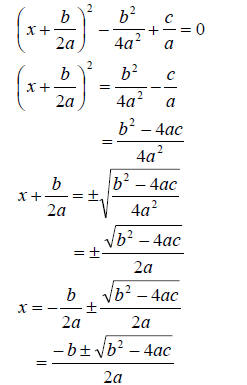
Example 2
A ball is thrown down at 50 mph from the top of a building. The building is 420
feet tall. Derive the equation that would let you find the time the ball takes
to reach the ground.
Solution
The distance covered by the ball is given by
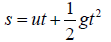
where
u= initial velocity (ft/s)
g= acceleration due to gravity (ft/s2)
t = time (s)
Given
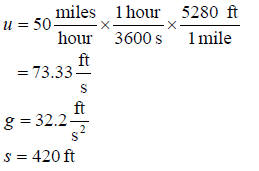
we have
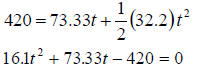
The above equation is a quadratic equation , the solution of which would give the time it would take the ball to reach the ground. The solution of the quadratic equation is
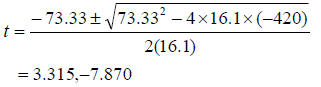
Since t > 0 the valid value of time is
.
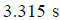| Prev | Next |