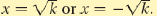Solving Quadratic Equations

What is a quadratic equation ?

The standard form of a quadratic equation is ax ² + bx + c = 0 , where a ≠ 0, b and
c are real numbers

Examples:

Ex. 12x² − 5x − 2 = 0

The Principle of Square Roots
 For any real number k, if x²=k , then

Ex. Solve
x² = 9
x² = 8
x² = −16

Ex. Solve
x² − 3 = 2
2x² = 36
2x² − 5 = −4
4x² +15 = 3

The Princtple of square Roots (Generalized Form)
  For any real number k and any algebraic espression x,
 If x²=k, then

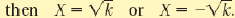
Ex. Solve…
(x − 3)² = 25
(x + 2)² = 4
(x +1)² = 12
(x − 5)² = −9
(5x − 3)² = 8

Ex. Given f (x) = x² − 6x + 2

a. Find f (−3)
b. Where is f (x) = −3

Ex. Given the function f (x) = x² − 6x + 2

a. Find the y-intercept
b. Find the x-intercepts

Completing the Square

Ex. Solve x ² −10x + 25 = 100

How to complete the square:
1. Start with x² + bx
2. Evaluate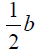
3. Evaluate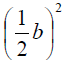

4. Combine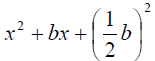

5. Factor, end up with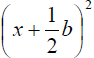

Ex. Complete the square

x² − 8x
x² +10x
x² −5x
x² + 7x

How to solve the equation ax²+bx+c=0  by first completing the square
1. If necessary, move c to the right-hand side of the equation
2. If necessary, divide both sides of the equation by a
3. Complete the square on the left-hand side
4. Balance the equation by adding 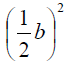  to right-hand side.
5. Factor and solve using Principal of Square Roots

Ex. Solve by completing the square

x² − 6x +1 = 15
x² +10x − 7 = 9
x² − 7x −3 =10
3x² −12x −8 = 25

Section 11.2 Quadratic Formula
Developing the formula…

The Quadratic Formula
 The solutions of ax²+bx+c=0,a≠0,aie give by
 

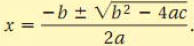
Ex. Solve…

2x² −9x + 5 = 0

Ex. Solve…

4x² = 3+ 7x
3x² + 2x = 7
12x² − 5x − 2 = 0

Ex. Given 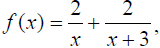   where is f (x) = 1?

Ex. Given f(x) = 2x²-5x+1
a. Find the y-intercept
b. Find the x-intercept(s), if they exist.

Which method to use ?
Factoring
Principal of Square Roots
Completing the Square
Quadratic Formula

Section 11.3 Formulas and Applications

Ex. Solve for d: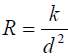

Ex. Solve for t: Y = rt ² − st

Ex. Sandi’s Subaru travels 280 mi averaging a certain speed. If the car had gone 5
mph faster, the trip would have taken 1 hr less. Find Sandi’s average speed.

Ex. A lot is in the shape of a right triangle. The shorter leg measures 120 m. The
hypotenuse is 40 m longer than the length of the longer leg. How long is the
longer leg?

Ex. The position of an object moving in a straight line is given by s(t) = −t ² + 8t ,
where s is in feet and t is the time in seconds the object has been in motion.
How long will it take the object to move 13 ft?

Section 11.6 Graphing Quadratic Functions

What is a quadratic function? What does its graph look like ?

• General Form
• Standard Form

The graph of a quadratic function/parabola
 

o Vertex
o Axis (or Line) of Symmetry
o Curvature
o Intercepts
o Min/Max Value

Ex. Graph f (x) = 2x² − 3
 

Vertex:
Axis of Symmetry Curvature
Min/Max Value

Ex. Graph f (x) = −2(x + 3)²

Ex. Graph f (x) = 3(x − 2)² +1

Ex. Graph f (x) = −4(x + 3)² − 2

Ex. Graph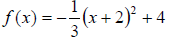

Ex. Graph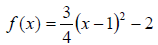
 

Section 11.7 More Quadratic Functions

General Form of Quadratic Function

Standard/ Vertex Form of Quadratic Function

How do you transform a quadratic function to standard form?

Ex. Write in standard form. f (x) = x² + 6x

Ex. Write in standard form. f (x) = x² + 4x + 3

Ex. Write in standard form. f (x) = x² − 8x + 23

Ex. Write in standard form. f (x) = 2x² +12x + 3

Ex. Graph the function by first finding the vertex, y-intercepts, x-intercepts (if
they exist) and any information about the shape
f (x) = 3x² − 24x + 43

Ex. Graph the function by first finding the vertex, y-intercepts, x-intercepts (if
they exist) and any information about the shape
f (x) = −4x² + 8x −1

The Vertex of a Parabola
 The vertex of the parabola given by f(x)=ax²+bx+c is
 
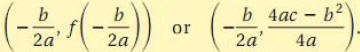
 The x-coordinate of the vertex is -b/(2a). The axis of symmetry is
 x= -b/(2a). The second coordinate of the vertex is most
  commonly found by computing

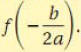
Section 11.8 Maximum and Minimum Problems

We have seen that for any quadratic function f, the value of f (x) at the vertex is either a
maximum or a minimum. Thus problems in which a quantity must be maximized or
minimized can be solved by finding the coordinates of the vertex, assuming the problem
can be modeled with a quadratic function.

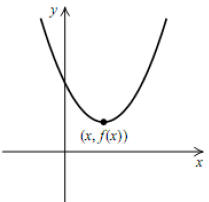
f(x) at the vertex a minimum


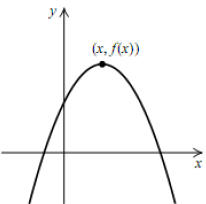
f(x) at the vertex a maximum

Ex. Find the maximum or minimum value of the function f(x)=x²-10x+21

Ex. Find the maximum or minimum value of the function f(x)= -3x²+6x+2

Ex. The value of a share of I. J. Solar can be represented by V(x)=x²-6x+13,
where x is the number of months after January 2004. What is the lowest value V(x)
will reach, and when did that occur?

Ex. Recall that total profit P is the difference between total revenue R and total cost C.
Given R(x) = 1000x -x² and C(x) = 3000 + 2x, find the total profit, the
maximum value of the total profit, and the value of x at which it occurs.

Ex. The perimeter of a rectangle is 40 inches. Determine the dimensions that
maximize the area of the rectangle.

Ex. A farmer has 200 ft of fence with which to form a rectangular pen on his farm. If
an existing fence forms one side of the rectangle, what dimensions will maximize
the size of the area?