Special Factoring Formulas and a General Review of Factoring

When the two terms of a subtractions problem are perfect squares, they are a special

multiplication pattern called the difference of two squares . Their pattern is:

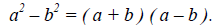
The knowledge of this patter will allow one to solve these special equations by knowing only what values were being squared in the original problem.

Example I: Factor x^2 – 25.

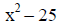	( find the values that were squared to get x^2 and 25)
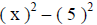	(apply the pattern shown above)
( x + 5 ) ( x – 5 )	(these are the factors)

Example II: Factor 4x^2 – 9.

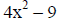	( find the values that were squared to get 4x^2 and 9)
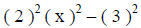	(apply the pattern shown above)
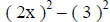	(continue)
( 2x + 3 ) (2x – 3 )	(these are the factors)

Example III: Factor 25x^2 - 16y^2

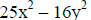	(find the values that were squared to get 25x^2 and 16y^2)
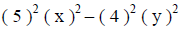	(apply the pattern shown above)
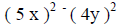	(continue)
( 5x + 4y ) ( 5x – 4y)	(these are the factors)

Where possible factor out any common factors, even if the factors are perfect squares , before applying the procedure.

Example IV: Factor 16x^2 – 64.

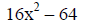	(16 is a factor of both terms and may be factored)
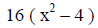	(apply the pattern)
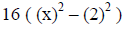	(continue)
16 ( x + 2 ) ( x – 2 )	(these are the factors of the problem)

Note: If you did not factor the 16 at the beginning of the problem, you would still get the correct answer since both terms are perfect squares:

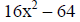	(apply the pattern)
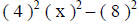	(continue)
( 4x + 8 ) ( 4x – 8 )	(factor out the common values in each term)
(4) ( x + 2) (4) ( x – 2 )	( combine like terms )
16 ( x + 2 ) ( x – 2 )	(these are the factors of the problem)

The principle of patterns applies to the sum and difference of cubes . Those patterns are:

Sum of cubes: a^3 + b^3 = ( a + b ) ( a^2 – ab + b^2 )
Difference of cubes: a^3 - b^3 = ( a – b ) ( a^2 + ab + b^2 )

NOTE: The second-degree term is always prime and should not be factored.

Example V: Factor x^3 + 64.

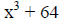	(this pattern is the sum of 2 cubes)
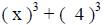	(these are the values that were cubed)
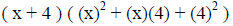	( perform all operations )
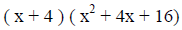	(these are the factors of the problem)

Example VI: Factor 8x^3 – 27y^3.

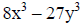	(this pattern is the difference of two cubes )
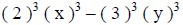	(these are the values that were cubed)
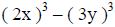	(continue)
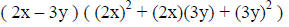	(perform all operations)
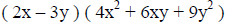	(these are the factors)

As seen in previous problems you may have to remove common factors to realize that you have one of these types of problems. Here are some further examples.

Example VII: Factor ( a + 2 )^2 – b^2 .

Recall that when anything is grouped is may be treated as a single term, no matter how much or little it contains.)

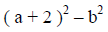	(since a + 2 is grouped it is a single term. This means that the problem may be treated as the difference of 2 squares.)
[ ( a + 2 ) + b ] [ ( a + 2 ) – b ]	(these are the factors.)

Example VIII: Factor 3x^2 – 75.

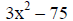	(since no pattern is apparent, we remove common factors.)
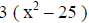	(now a pattern appears, the difference of 2 sq.)
3 ( x + 5 ) ( x – 5 )	(these are the solutions to the problem .)

Example IX: Factor a^4 – b^4

Applying the exponential law 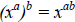each term may be rewritten.

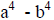	(apply the exponential law )
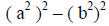	(the difference of 2 squares pattern is used)
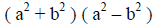	(continue)
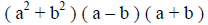	(these are the solutions)

NOTE: ( a^2 + b^2 ) is the sum of two squares for which there are no real solutions. The pattern of the difference of two squares cannot be made to apply to it.