What is a Square Root?
Do you remember learning about square roots in middle
school and high school?
Were they ever really confusing or some parts were
always left unexplained. Like,
why can’t you take the square root of a negative
number? These questions are
actually quite common and relatively simple to
answer.
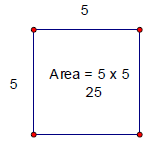
| One good way to understand square roots is to first look
at squares. In a square, to find the area you can simply take one side times itself to get to the total area of the |
|
| square. In the picture we have the side
of the square is 5 and the area is therefore 5 x 5 which is 25. We then say that 25 is the “square” of 5. The square of any number is simply the number times itself. We write this as 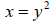 for y being an for y being an integer. For example, 4, 7, and 13 as values of y give you squares of 16, 49, and 169 for values of x. |
 |
Now we would like to look at this situation backwards.
Given a number like 64 for
x, what is the value of y so that 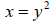 . This value is the square root
of x. Which
. This value is the square root
of x. Which
we use the sign 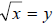 , also called a radical. The radical also implies
that this
, also called a radical. The radical also implies
that this
result is positive. For example, when we take the square root of 9 we
actually get
two numbers, 3 and (-3), that are roots of 9. We recognize this as
taking a square
root as meaning 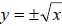 . Taking the square root of a number always
gives you
. Taking the square root of a number always
gives you
two distinct answers.
 |
Historically, the square root was one of the most studied objects, especially in terms of irrationability. Around 2000 BC the Babylonian tablet YBC 7289 contained 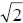 to 9 to 9 significant decimals. This tablet gives the number 1, 24 51 10 which, in base 60, is very close the square root of 2. The Pythagoreans proved that 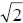 is irrational, despite their is irrational, despite their
belief that all number were rational and could be represented as a ratio of two integers. Legend has it that the Pythagorean Hippasus made this |
| discovery while out at sea. He caused such an uproar that
they decided to throw him off the boat rather than let his discovery be known. However, Theodorus later proved that the numbers 3-17 were irrational, except for 4, 9, and 16. |
|
The radical was not always used as a sign for the square root. In 1220 Leonardo
of
Pisa used the symbol Rx, similar looking to a prescription symbol . The
emergence
of the radical happened later around 1525 as what looked like a
checkmark without
the line above . In 1629 Albert Girard suggested placing the
index in the small
opening of the checkmark part. Thus a cube root would be
written as 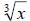 . It was
. It was
not until Rene Descartes in 1637 did we have our
traditional symbol for the radical
with the checkmark part and the line over the
top. The last development for the
square root was that in 1895 it decided that 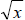 would represent one value rather
would represent one value rather
than two.
Proving that
![]() is irrational
is irrational
One of the most interesting properties of square roots is
for integers, the result is
either another integer or irrational. The Greeks
believed that all numbers could be
represented as the ratio of two integers .
However, it was eventually proved that
the square root of 2 cannot be
represented in this way. Here are two short proofs
that show
![]() is irrational.
is irrational.
If
![]() were rational then it can be represented by the ratio of integers p and q
in
were rational then it can be represented by the ratio of integers p and q
in
this way; 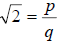 . Using algebra we can square both sides and multiply by
. Using algebra we can square both sides and multiply by
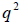 to
to
get
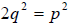 . By the fundamental theorem of algebra we know that p and q have a
. By the fundamental theorem of algebra we know that p and q have a
unique
factorization. Looking on the left-hand side we can see that no matter
what,
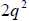 factors down to an odd power of 2, while the RHS factors down to an
factors down to an odd power of 2, while the RHS factors down to an
even power
of 2. This contradicts that they must be equal and therefore our
assumption that
![]() is rational is incorrect.
is rational is incorrect.
| Another way is by using an isosceles-right triangle. Showing two sides are | |
|
commensurable means that there is some integer length that divides both sides which implies that the ratio of sides is a rational number. If we show that the sides are incommensurable it is equivalent that those sides cannot be expressed as a rational number. Assume that we have some integer m so that m|AB and m|BC. We then make DB=AB so m|DB. It then follows that BC=CD+DB so |
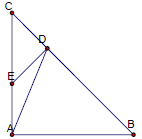 |
| m|CD. Segment DE is constructed so that DE is
perpendicular to BC and we have similar triangles ABC and DEC by AA. We then have <EAD+<DAB=90 and <EDA+ADB=90, and since ABD is isosceles we have <ADB=<DAB so it follows that <EAD and <EDA are supplementary to the same angle, therefore they must also be equal. So triangle EDA is isosceles and we have that m|CD and CD=DE=EA so m|EA. It follows that CA = CE+EA and m|CE. We have therefore proved that m|CE and m|CD therefore we have an isosceles-right triangle with smaller dimensions than before whose lengths are divisible by m. We can continue this construction for a smaller yet isosceles-right triangle, but eventually we will reach a value for a side that is less than m. Since m cannot divide a number less than itself we can see that our original assumption m|AC and m|CB is false and sides AC and CB are incommensurable. By the Pythagorean theorem we can show this ratio is 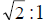 . . |
|
Calculating Square Roots
Now some of you might be wondering, how did they find the
values of square
roots, if they didn’t have calculators? There are actually many
different ways that
they had available, using either algebra or geometry.
| The Greeks were very interested in geometry, therefore
their way of finding square roots involved constructing them on paper using a compass and straightedge. Let’s |
|
|
use their method to find the square root of 7. First we draw a line AB of length 7. We then make C so that AC = 1. Either by calculation or construction we make D which is the midpoint of BC and then draw a circle with D as the center and the radius as DB or DC. Lastly, we make a perpendicular line from A which intersects the circle at E. The length of AE is now the square root of 7. This method actually comes from the geometric mean of two numbers. Usually the geometric mean of 2 and 5 for example is 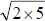 . In the picture . In the picture |
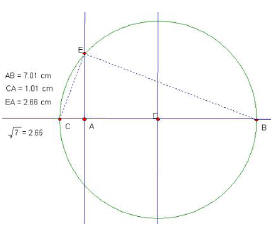 |
it would be expressed as
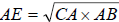 . We had CA = 1 so we
were left with just . We had CA = 1 so we
were left with just the square root of length AB. |
|
| Around 1655 the popular method of computing the square root involved a | |
|
continued fraction. In order to calculate the square root of 2 you would take compute the expression on the right . This infinite fraction would get closer and closer to the square root of 2 as you continued on the calculation. This is usually represented as {1, 2, 2, 2…}. It can be shown that all integer |
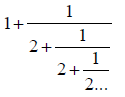 |
| square roots can be represented in this way and their form
with be periodic, that is the number sequence in the chain of fractions will repeat. For example the square root of 3 is represented as {1, 1, 2, 1, 2, 1, 2…}. This method worked very well, but we not near as efficient as the next method. |
|
Isaac Newton developed a method that is very commonly used
today called simply
Divide and Average. This is a recursively defined
function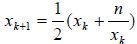 where
where
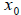 is some guess. This method is very efficient in
quickly calculating a square
is some guess. This method is very efficient in
quickly calculating a square
root. The guess is not so important in coming up
with the final result. Often it
takes only 3 or 4 iterations before the fraction
covers 8 or 9 digits of accuracy.
Next is the question that many people wonder quite
frequently. How does my
calculator do the square root? Does it use one of these
methods? Actually your
calculator has its own way. Your calculator has very well
defined functions for
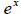 and
and 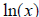 . We combine the identities
. We combine the identities
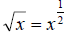 and
and 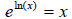 to get
to get
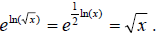
Lastly we have roots of imaginary numbers. The imaginary
number i is defined as .
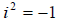 We use this definition to take the square root of
negative numbers, for
We use this definition to take the square root of
negative numbers, for
example -36. We initially learn in school that we cannot
evaluate 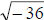 , but by
, but by
using our definition we can rewrite this as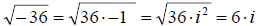 . Another
. Another
way you can think of it is to simply take the
square root of the absolute value and
then multiply it by i. We can use any of
the methods we already know to do this.
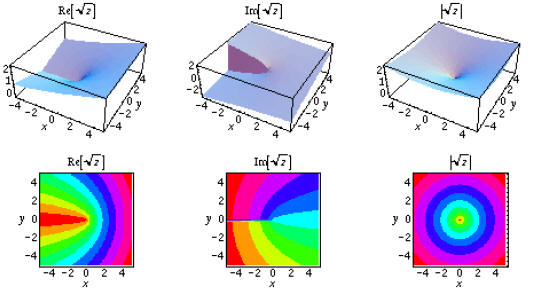
These methods cover how to take the square root of any
real number or imaginary
number in a simple way, but how do we take the root of
a complex number ? I
asked a group of college mathematicians and they did not
have an answer for me.
This is rarely covered in secondary or even
post-secondary education, but it still
make you wonder “How do you do it?” We
actually go back to our original
definition of the square root as the inverse of
the function ![]() . Suppose we want
. Suppose we want
to find the square root of 5 + 6i. We want to
find some y = a + bi such that
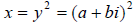 Expanding
Expanding
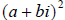 we get
we get 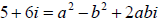 . Our real part is
. Our real part is
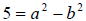 and the imaginary part
is
and the imaginary part
is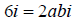 . We can then solve these
two
. We can then solve these
two
equations for a and b which gives us our solution (s). We can also do this
computation in polar coordinates by knowing that
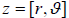 and by a theorem we
and by a theorem we
get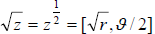 . Polar coordinates also makes it easier to extend this idea
. Polar coordinates also makes it easier to extend this idea
into
cube, quartic, and nth roots.
| Prev | Next |