Write Linear Equations in Point-Slope Form
Warm up
1) Write an equation of the line that passes through (3, 4), m = 3
2) Write an equation of the line that passes through (-2, 2) and (1, 8)
3) A carnival charges an entrance fee and a ticket fee. One person paid $27.50
and bought 5
tickets. Another paid $45 and bought 12 tickets. How much will 22 tickets cost?
Consider the line that passes through the point (3, 4)
with a slope of3. Let (x, y) be another point
on the line. You can write an equation relating x and y using the slope formula ,
with
(x1, y1) = (3, 4) and (x2 , y2 ) = (x, y) .
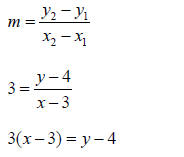
The equation in point- slope form is y − 4 = 3(x − 3) .
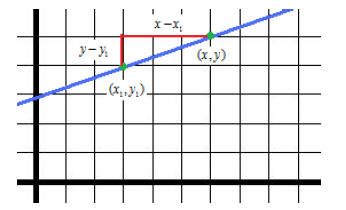
The point-slope form of the equation through a given
point (x1 , y1 ) with a slope m is y − y1 = m(x − x1) .
Ex 1) Write an equation in point-slope form of the line
that passes through the point (4, -3) and
has a slope of 2.
y − y1 = m(x − x1)
y + 3 = 2(x − 4)
Practice: Write an equation in point-slope form of the
line that passes through the point (-1, 4)
and has a slope of -2.
Ex 2) Graph the equation
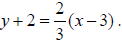
Because the equation is in point-slope form, you know that the
line has a slope of 2/3 and passes through the point (3, -2). Plot
the point (3, -2). Find a second point on the line using the slope.
draw a line through both points.
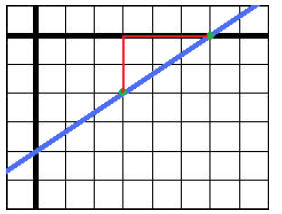
Practice: Graph the equation y −1 = −(x − 2)
Ex 3) Write an equation in point-slope form of the line
shown.
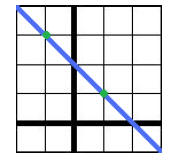
Step 1: Find the slope of the line
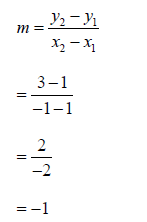
Step 2: write the equation in point-slope form. You can use either given point.
y − y1 = m(x − x1)
y − y1 = m(x − x1)
y − 3 = −(x +1)
y −1 = −(x −1)
Check that the equations are equivalent by writing them in slope- intercept form .
Practice: write an equation in point-slope form of the
line that passes through the points (2, 3)
and (4, 4).
Ex 4) you are designing a sticker to advertise your band.
A company charges $225 for the first
1000 stickers and $80 for each additional 1000 stickers . Write an equation that
gives the total
cost (in dollars) of stickers as a function of the number (in thousands) of
stickers ordered . Find
the cost of 9000 stickers.
Step 1: Identify the rate of change and a data pair. Let C
be the cost (in dollars) and s be the
number of stickers (in thousands).
Rate of change , m: $80 per 1 thousand stickers
Data pair, ( s1,C1 ): (1 thousand tickets, $225)
Step 2: write an equation using point-slope form. Rewrite
the equation in slope- intercept form so
that the cost is a function of the number of stickers .
C −C1 = m(s − s1 )
C − 225 = 80(s −1)
C = 80s +145
Step 3: Find the cost of 9000 stickers
C = 80(9) +145 = 865
The cost of 9000 stickers is $865
Homework: A#40 pg. 297 # 23-28 pg.306 14-28
| Prev | Next |