Introduction to Linear Algebra
Recall we have previously defined the determinant of a 2 ×
2 matrix
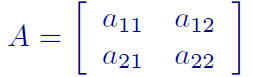as 
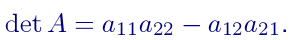How
was this use in the
formula for the inverse of a 2 × 2 matrix?
The determinant of any matrix A is usually denoted by either |A| or detA.
We may also write
We essentially replace the bracket notation [ ] around the matrix with
absolute value type notation | |, indicated we want the determinant of the
matrix.
We define the determinant of a 1 × 1 matrix A as
where |a| does NOT indicate absolute value.
Determinant of a 3 × 3 Matrix
The determinant of a 3 × 3 matrix can be thought of as a linear combination
of determinants of 2 × 2 matrices. The process is exactly the same as the
cross product .
Then the determinant of A is the scalar
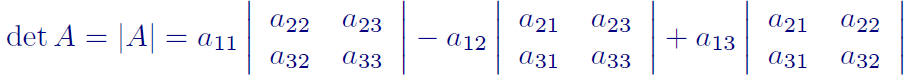
We define the (i, j) minor of A, Aij , as the submatrix of A obtained by
deleting row i and column j. We may then write
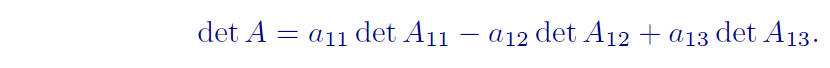
Ex: Find the determinant of
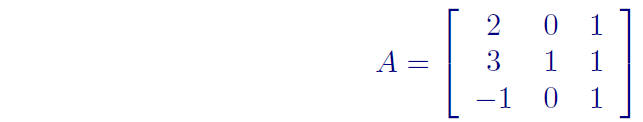
Determinant of an n × n Matrix
Let A = [aij ] be an n × n matrix, n ≥ 2. Then the determinant of A is
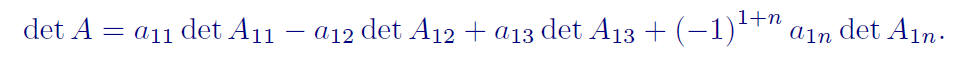
The minor with its sign , is the (i, j)− cofactor of A :
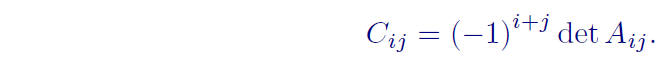
Then we may write
Interestingly, the determinant can be computed similarly using any other row.
Laplace Extension Thm: An n × n matrix A = [aij ], n ≥ 2 has
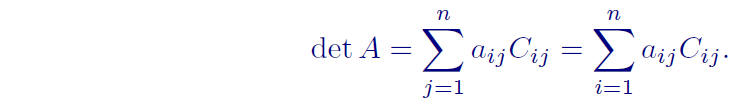
These are the cofactor expansion along the ith row and jth column,
respectively
Computing determinants
Ex: The previous theorem tells us that we may choose any row or column to
compute the determinant along. Use this idea to find the determinant of
each of the following:
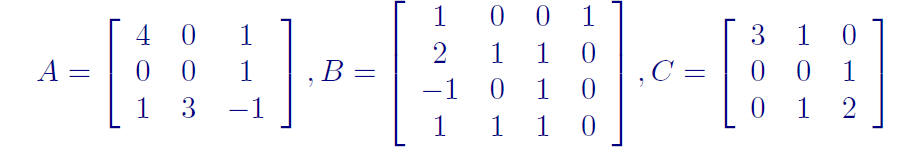
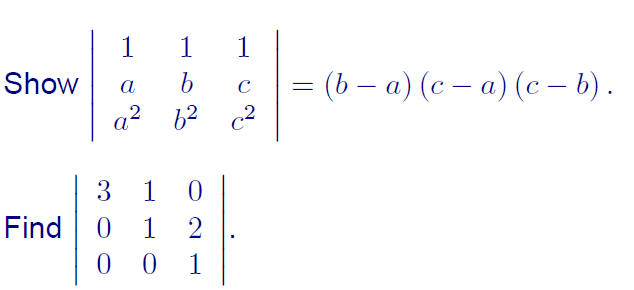
Properties of determinants
Thm: Let A = [Aij ] be a square matrix.
(a) If A has a zero row (column), then detA = 0.
(b) If B is obtained by interchanging two rows (columns) of A, then
detB = −detA.
(c) If A has two identical rows (columns), then detA = 0.
(d) If B is obtained by multiplying a row (column) of A by k, then
detB = l detA.
(e) If A,B and C are identical except that the ith row (column) of C is the
sum of the i th rows (columns) of A and B, then detC = detA + detB.
(f) If B is obtained by adding a multiple of one row (column) of A to
another row (column), then detB = detA.
Ex: Compute detA for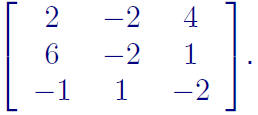
Ex: Compute detA for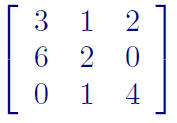
by
reducing to rref . Remember to keep
track of scalars!
Determinants of Elementary Matrices
Thm: Let E be an n × n elementary matrix.
(a) If E results from interchanging two rows of In, then detE = −1.
(b) If E results from multiplying one row or In by k, then detE = k.
(c) If E results from adding a multiple of one row of In to another row, then
detE = I.
Lemma: Let B be an n × n matrix and E be an n × n elementary matrix.
Then
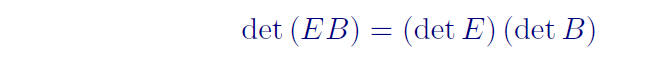
The previous theorem and lemma can be used to prove the following
Thm: A square matrix A is invertible iff detA ≠ 0.
Pf: The idea is the you reduce A to rref R using elementary matrices
E1, . . . ,Er. Write
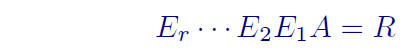
and take the determinant of both sides.
Determinants and Matrix Operations
Thm: If A is an n × n matrix, then det (kA) = kn detA.
Note: In general, there is no formula for det (A + B).
Thm: If A and B are n × n matrices, then
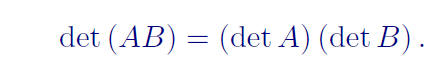
Ex: For A =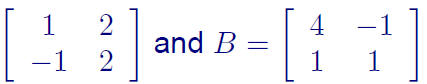
find det AB by first calculating AB and finding its determinant, and then by
using the theorem.
Thm: If A is invertible, then
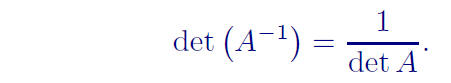
Ex: Find det (A−1) for A from the previous exercise by
explicitly finding A−1
and by using the previous theorem.
Aside: Cramer’s Rule and the Adjoint
The book presents Cramer’s Rule, which allows you to solve small matrix
problems easily. The idea is that we can find the solution to a linear system
simply from computing determinants.
The text also presents the adjoint of a matrix. These can both be used to
help prove the Laplace Expansion Theorem. Their practical application is
limited, thus we will discuss these in class only if time allows. If you are a
Math major, make sure you read through each of these concepts.
The last theorem for this chapter is used as part of the proof of the Laplace
Expansion Theorem:
Thm: Let A be an n × n matrix and let B be obtained by interchanging any
two rows (columns) of A. Then
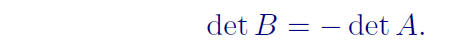
Matlab Determinants
As with most subjects in linear algebra , Matlab has a very intuitive way to
compute the determinant. We simply define a matrix, and apply the function
det. To find the determinant of
we do:
» A = [3,1,2;3,1,0;0,1,4];
» det(A)
Let us say we wish to verify det (A10)= (detA)10. We do:
» A = [3,1,2;3,1,0;0,1,4];
» det(A^10)
» det(A)^10
| Prev | Next |