A non-measurable set in (0,1]
Let "+" stand for addition modulo 1 in (0, 1]. For
example, 0.5 + 0.7 = 0.2,
instead of 1.2. If A ⊆ (0, 1], and x is a number , then
A+x stands for the set of
all numbers of the form y + x where y ∈ A. You may
want to visualize (0, 1] as
a circle that wraps around so that after 1, one starts again at 0.
Define x and y to be equivalent if x +r = y for some
rational number r. Then,
(0, 1] can be partitioned into equivalent classes . (That is, all elements in the
same equivalence class are equivalent , elements belonging to different
equivalent
classes are not equivalent , and every x ∈ (0, 1]
belongs to some equivalence
class.) Let us pick exactly one element from each equivalence class, and let
H be the set of the elements picked this way. (This fact that a set H can be
legitimately formed this way involves the Axiom of Choice, a generally accepted
axiom of set theory.) We will now consider the sets of the form H + r, where r
ranges over the rational numbers in (0, 1]. Note that there are countably many
such sets.
The sets H + r are disjoint. (Indeed, if r1 ≠ r2 and H +
r1 and H + r2
share the point h1 + r = h2 + r2, then h1 and h2 differ by a rational
number
and therefore are equivalent . If h1 ≠ h2, this contradicts the construction of
H,
which contains only one element from each equivalence class. If h1 = h2, then
r1 = r2, which is again a contradiction.) Therefore, (0, 1] is the union of
the
countably many disjoint sets H + r.
The sets H + r for different r are "translations" of each
other (they are all
formed by starting from the set H and adding a number . The "uniform" proba-
bility measure (or Lebesgue measure) assigns a probability to each interval
equal
to its length, so that when an interval is a translation of another, they should
have the same probability. We are interested in whether Lebesgue measure can
be defined for all subsets of (0, 1], while remaining translation-invariant. If
this
were possible, each set H +r should have the same probability, and their prob-
abilities should add to 1. But this is impossible, since there are infinitely
many
such sets.
A stronger statement is actually true, but harder to
prove. there exists no
probability measure on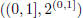 
under which P({x}) =
0 for all points x.
The Banach-Tarski Paradox. Let S be the
two-dimensional surface of
the unit sphere in three dimensions. There exists a subset F of S such that for
any k ≥ 3,
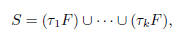
where each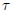 
is a rigid
rotation. For example, S can be made up by three rotated
copies of F (suggesting probability equal to 1/3, but also by four rotated
copies
of F, suggesting probability equal to 1/4). Ordinary geometric intuition clearly
fails when dealing with arbitrary sets.
| Prev | Next |