Algebra and Geometry Sample Prob
Algebra and Geometry Sample Problems
Algebra 1
Reasoning. State whether the following statement is sometimes, always, or never
true and explain
your answer with an example or counterexample. Systems of inequalities made up
of parallel lines
have no solutions .
Answer: Sometimes. If the system is 2x + 3y > 5 and 2x + 3y is < 7 the points
between the two lines
would be solutions.
Reasoning. Identify the system of equations whose solution is not similar to the
other three.
Answer: The third set. This system has no solution. The
lines parallel .
Geometry
Challenge. Describe the family of functions that define this translation.
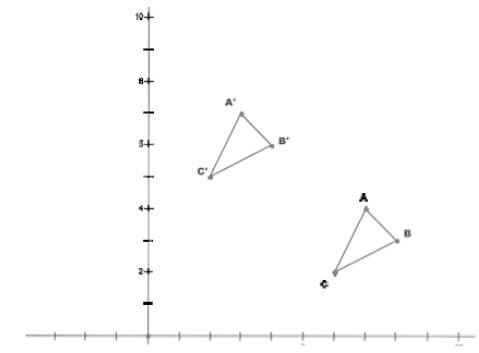
Answer: Use the formula for slope to find the slope of any
pair of corresponding points. Use the
slope intercept form to write a general equation: y = 3/-4x + b
Challenge: Use the enlarged internal dilation that begins
with the figure to the right
and your knowledge of dilations to explain that the sum of the
geometric series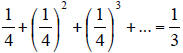
is true
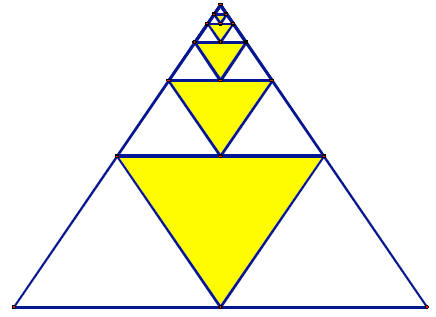
Answer. Proof Without Words
If your look at teach layer, one of three triangles is shaded which represents
1/3 of the total area.
Algebra 2
Writing in Math : Describe the method used to find the equation of a circle if
the endpoints of the
diameter are given.
Answer: First you should find the center of the circle which is the midpoint of
the diameter. Next
calculate the length of the radius using the distance formula from the radius to
one of the points on the
diameter. Finally substitute the values of the center, one endpoint of the
diameter, and the length of
the radius into the general equation for the circle (x -h)2 + (y + k)2 = r2.
Writing in Math : Explain if you are graphing a hyperbola from an equation , one
of be best ways to
draw a representative sketch is by graphing the asymptotes of a hyperbola.
Answer: The graphs of the asymptotes of a hyperbola provide boundaries for the
hyperbola. If the
equation is given, the center, and values of a and b are available . The foci, ±
c, can be found using
the Pythagorean Theorem. Graphing the asymptotes gives a frame for the
hyperbola.
| Prev | Next |