An Introduction to Matlab: Part 4
This lecture assumes that you have already worked through parts 1-3. You
should be able to create and use script les,
create and use vectors, and understand the concept of component wise arithmetic .
This part covers
• Creating Matrices
• Manipulating matrices
• Matrix addition and multiplication
• Solving Ax = b
• Using matrix functions
In this part, and in future parts, we will do a bit less hand-holding and let
the user attempt to figure how most things
themselves.
Creating matrices
This section goes through creating matrices by typing each element, using patterns, and by using a few built-in functions.
1. Typing in matrices explicitly: Here we learn how to type matrices.
(a) Open Matlab. If you already have it open, type clear all; in the Command
Window. I would do everything in the
Command Window for now so you don't have to rerun you le everytime we make a
change.
(b) Luckily, since you know how to create row and column vectors, creating a
matrix is easy. Recall that putting a
space or comma between elements in bracket notation [] means to change rows.
Putting a semicolon means to
change columns . To form a matrix, simply combine the two . Type
A=[1 2; 3 4]
This says the first row is 1 2, the second row is 3 4. Use this idea to create each of the following:
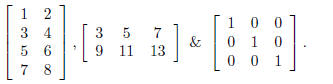
(c) Try typing
A=[1 2; 3 4 5]
You get a vertcat (vertical concatination) error. Why? Because you tried to make
the first row have only 2
columns and the second row have 3 columns. A matrix must have the same number of
columns per row (or rows
per column).
2. Creating a zero matrix , ones matrix, identity matrix, or random matrix:
Here we discuss how to create a matrix of all
zeros, all ones, completely random entries (between 0 and 1), and how to create
an identity matrix.
(a) To create a matrix of all zeros, we use the zeros function. It takes two
(for now) arguments. These represent the
size of the matrix you wish to create. Type:
A = zeros(5,4)
You get a 5 × 4 zero matrix. Try creating a zero matrix of size 10 × 10.
(b) To create a matrix of all ones, we use the ones function. It has the same
structure as the zeros function:
B = ones(4,5)
(c) You can create a matrix with random entries (these random entries are
randomly drawn from between 0 and 1)
using the rand function:
C = rand(5,5)
(d) To create an identity matrix we use the eye function:
I = eye(5,5)
Manipulating matrices
This section tells how to manipulate a given matrix and how to create new
matrices from other matrices.
1. Changing and adding matrices: Here we'll learn how to change parts of a given matrix.
(a) Suppose we want to create an elementary matrix of size 5×5 that
interchanges the first and last elements. So we
want the matrix

We can type in each of the 25 entries of this matrix, or we can simply modify
the identity matrix, or a zero matrix.
Let us start by modifying the identity matrix to what we want:
E = eye(5,5)
Now, we need to change the first row, and the last row. We can either change
the whole row, or just change the
needed elements. I would change the elements by typing:
E (1,1)=0; E(1,5)=1; E(5,5)=0; E(5,1)=0
Try to create the E given above by starting with a zero matrix.
(b) Just like with vectors , I can add rows or columns to a given matrix.
Suppose, given the E above, we wish to add
a row of all zeros (turning E into a 6 × 5 matrix). Try:
E(6,:)=0;
The colon notation in the second index of the matrix means ALL columns. So, for
row 6 and each column of E,
this assigns a zero.
We are not restricted to just adding one column or one row. Let us take the
current E (which is 6 × 5) and turn
it into a 6 × 7 matrix will all ones in the last two columns . We do:
E(:,[6 7]) = 1;
2. Extracting a submatrix and combining matrics: Here we extract part of a
matrix to create a new matrix, and combine
two matrices into a larger matrix.
(a) We extract elements from a matrix to create a new matrix, just like with
vectors. Recall that with a vector v of
size 5, if I wanted a new vector u containing the 1st, 4th and 5th elements, I
type: u=v([1 4 5]). We use the same
idea for matrices. Create A to be a 5 × 5 identity matrix. Suppose we want to
create a matrix B that contains
every row of A, but only the 1st, 2nd and 4th column. We do:
B=A(:,[1 2 4]);
Try to create a marix C that contains the 1st and 3rd rows of A, and the 4th and
5th columns. What matrix do
you get?
(b) We can also enlarge a matrix by combining two matrices (or a matrix and a
vector, or even a vector and a vector).
We again do this the same way as with vectors, but we need to be careful about
sizes now. Create A to be the
5 × 5 identity, B to be a random 5 × 4 matrix, and C to be a random 4 × 5
matrix. Try each of the following:
[A B]
[A ; B]
[A C]
[A ; C]
[B C]
[B ; C]
We find, just like with vectors, if we type [A B] then this adds the matrix B
into columns after the matrix A
(making a 5×9) matrix. [A;B] attempts to add B as rows after A, but A has 5
columns and B only has 4 columns.
Recall we cannot have a row with a different number of columns than the other
rows. The same idea holds for
each of the other operations. We can combine the ideas here with those in (c)
and try:
[A B(:,[3 4])]
Matrix addition and multiplication
Matrix addition and multiplication behave exactly as one would expect. The
only thing we need to be careful of is that the
sizes are correct for the defined operations.
1. Matrix addition: Here we discuss linear combinations of matrices
(a) Type clear all. Create A and B as 3 × 3 random matrices and C as a 3 × 4
random matrix.
(b) Compute 2A − 3B. Try to compute A − C. What happens?
2. Matrix multiplication: Here we discuss matrix-matrix multiplication,
matrix-vector multiplication, vector-matrix mul-
tiplication, and matrix-matrix componentwise multiplication.
(a) Create two 3 × 3 matrices: A = [1 2 0; 2 0 1; -1 1 1] and B = [1 0 1; 0 1
0; 2 0 2]
(b) Compute AB by typing A*B. Compute BA. Are they the same? Should they be?
(c) Create a column vector b=[1 ; 2 ; 3] and a row vector c=[1 2 3].
(d) Compute Ab by typing A*b. Note that we get a column vector, as expected. Try
to compute Ac. Why does this
not work? What should A*[1;0;0] return?
(e) Compute cA. Try to compute bA as well.
(f) Type A.*B. Type B.*A. Did you get the same thing? Why is this so, since in
part (b) we showed AB ≠ BA?
Solving Ax = b
There are multiple ways to solve the traditional matrix problem Ax = b in Matlab. We discuss two ways.
1. We'll use the same A and B from the previous section . Recreate them if
needed. Let b=[7;7;7].
2. Using the inverse of A.
(a) We can solve the problem Ax = b (or Bx = b) by explicitly computing the
inverse. To do this, we use the inv
command. Assign A inv to be the inverse of A by typing
Ainv = inv(A)
(b) Now, we simply need a matrix-vector multiplication: x = A−1b. Do this.
Remember this answer for later.
(c) Try to compute B−1. What happens? The Inf values mean the matrix has gone to
infinity, and the Warning:
Matrix is singular to working precision mean the matrix is not invertible (it
actually means the computer cannot
evaluate the inverse, but for our purposes they are the same thing).
3. Using Gaussian Elimination . (Preferred way to solve Ax=b)
(a) There is a very easy construct for solving Ax = b in Matlab. It is called
the left divide and is denoted by \ . The
reason it is called this is because to solve Ax = b we are essentially dividing
the left side of each equation by A.
In reality , when you use left divide Matlab performs Gaussian Elimination with
partial pivoting on your linear
system . In Matlab, this is denoted
x=A\b
(b) Try to solve Bx = b using Gaussian Elimination. Note you get the same
error as when you tried inv(B), but now
you get a different answer. The Nan entries mean Not a number.
Using matrix functions
There are many functions which act on matrices. Most any function that can
act on a scalar or vector can also act on a
matrix. Most functions we will simply list and not describe in any detail. Use
help or doc to find more information.
1. Compute abs(A), sin(A), sqrt(A), and exp(A). Note that each function acts
componentwise on the matrix A. This is
important, as the matrix exponential and a matrix square root have different
meanings than componentwise arithmetic
(they are funtions expm and sqrtm, respectively).
2. Matrix transpose: To compute the transpose of a given matrix A, we use the
same construct as computing the transpose
of a vector. We use A'. Compute ATA and

3. Functions for determining if an inverse exists: Here we brie y list some
functons that can be used in determining if an
inverse exists.
(a) Use rank(A) to approximate the rank of A.
(b) Use det(A) to compute the determinant of A.
(c) Use rref(A) to compute the reduced row echelon form for A.
(d) Use null(A) to compute the null space of A.
(e) Use inv(A) to try to find the inverse of A.
4. As with vectors, you can find the size of a matrix A by typing [n,m]=size(A) .
5. Later in the class, you will want to find eigenvectors and eigenvalues of a
matrix. To do this we use the eig fuction. It
returns two matrices. The first contains the eigenvectors as columns, and the
second is a diagonal matrix that contains
the corresponding eigenvalues. Try:
[V D] = eig(A)
You can extract the eigenvalues as a vector if you would like by typing
d=diag(D)
Which takes d to be a vector of only the diagonal of D. Verify that Av1 = d1v1
where d1 is the first eigenvalue and v1
is the first eigenvector.
6. Execute the following commands and try to figure out what
each one does to the matrix A: min(A), min(A'),
min(min(A)), sum (A), sum(A'), sum(sum(A)), prod(A), prod(prod(A)), A<0, A>0,
A==0
| Prev | Next |