CALCULUS Curriculum Guide

PROFICIENCY 1: THE LEARNER WILL DEVELOP AN UNDERSTANDING OF
FUNCTIONS AND GRAPHS

1.1 Define functions from problematic situations

1.2 Determine whether a given function is even or odd

1.3 Determine the zeros of a function

1.4 Graph trigonometric functions and determine their periods, amplitudes, and phase shifts

1.5 Find the slope of a linear function

1.6 Use the standard forms to write an equation of a line that fits given conditions

1.7 Graph exponential and logarithmic functions and use their inverse relationships

1.8 Find the asymptotes of the graph of a function

1.9 Describe the symmetry of the graph of a function

PROFICIENCY 2: THE LEARNER WILL DEVELOP AN UNDERSTANDING OF LIMITS
AND CONTINUITY

2.1 Find or approximate limits intuitively using a calculator

2.2 Find limits of functions by substitution

2.3 Find limits using the constant, sum, difference , product , and quotient rules

2.4 Find the limit of a rational function that has an indeterminate form

2.5 Find one-sided limits

2.6 Find limits at infinity

2.7 Determine when a limit is infinite

2.8 Use the definition of continuity to determine whether a function is continuous at a point

2.9 Use the intermediate value theorem on a function over a closed interval

2.10 Determine the types of discontinuities of a function

2.11 Apply the theorem, “If f (x) is continuous over a closed interval, then f has a maximum
and a minimum value on the interval”

PROFICIENCY 3: THE LEARNER WILL DEVELOP AN UNDERSTANDING OF THE
CONCEPTS OF DIFFERENTIAL CACLULUS

3.1 State and apply the definition of derivative

3.2 Find the derivatives of elementary functions including algebraic , trigonometric,
exponential, and logarithmic

3.3 Find the derivatives of sums, products, and quotients

3.4 Determine the derivative of a composite function ( chain rule )

3.5 Find the derivatives of implicitly defined functions

3.6 Find derivatives of higher order

3.7 Find the derivative of the inverse of a function

3.8 Find derivatives using logarithmic differentiation

3.9 Use the relation between differentiability and continuity

3.10 Apply the Mean Value Theorem

3.11 Use 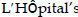Rule

PROFICIENCY 4: THE LEARNER WILL DEVELOP AN UNDERSTANDING OF THE
APPLICATIONS OF THE CONCEPTS OF A DERIVATIVE

4.1 Find the slope of a curve

4.2 Find the tangent and normal lines

4.3 Determine where a function is increasing and where it is decreasing

4.4 Find critical points, relative (local), and absolute maximum and minimum points

4.5 Determine the concavity and points of inflection of a function

4.6 Use first and second derivatives to help sketch a curve

4.7 Use differentials to approximate change

4.8 Use Newton’s Method to approximate the zeros of a function or the intersection of two
functions

4.9 Solve optimization problems

4.10 Find average and instantaneous rates of change

4.11 Find the velocity and acceleration of a particle moving in a straight line

4.12 Find related rates of change

PROFICIENCY 5: THE LEARNER WILL DEVELOP AN UNDERSTANDING OF THE
CONCEPTS OF INTEGRAL CALCULUS

5.1 Use rectangle approximation techniques to find approximate value of integrals

5.2 Calculate the values of Riemann Sums

5.3 Recognize and write definite integrals as limits of Riemann Sums and vice versa

5.4 Use the Fundamental Theorem of Calculus

5.5 Use properties of antiderivatives and the Fundamental Theorem of Calculus to evaluate
definite and indefinite integrals

5.6 Use properties of definite integrals

5.7 Use the technique of integration by substitution ( change of variables ) to find values of
integrals

5.8 Use the technique of integration by parts

5.9 Use the technique of integration by trigonometric substitution

5.10 Use numeric techniques such as the Trapezoidal Rule, Simpson’s Rule, or technology to
approximate definite integrals

PROFICIENCY 6: THE LEARNER WILL DEVELOP AN UNDERSTANDING OF THE
APPLICATIONS OF INTEGRAL CALCULUS

6.1 Derive velocity functions from acceleration functions and/or position functions from
velocity functions given the necessary initial conditions

6.2 Solve separable differential equations of the form f (x)dx = g (y)dy

6.3 Solve differential equations of the form y’ = k y as applied growth and decay problems

6.4 Use definite integrals to find the area under a curve and above the x-axis

6.5 Use definite integrals to find the area between two curves

6.6 Use definite integrals to find the average value of a function over a closed interval

6.7 Use definite integrals to find the volume of a solid with known cross-sectional areas

6.8 Use definite integrals to find the volume of a solid obtained by revolving an area about the
x-axis, y-axis, or a line parallel to either axis (Disc, washer, and shell methods)

6.9 Use definite integrals to calculate the surface area of a solid obtained by revolving a region
about one of the coordinate axes

6.10 Write improper integrals as limits of definite integrals to determine their nature (convergent
or divergent) and find the values of those that converge