CALCULUS REVIEW
In this course we will encounter problems requiring
calculus, especially dif-
ferentiation. I have prepared the following as a review of the material you have
learnt in a basic course on calculus.
1. Simple Power Functions
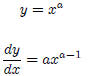
For example if a = 1, then
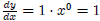. If a = 10, then
:
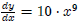2. Sums, Differences and Constants :
Example 1:
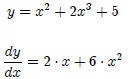
Example 2:
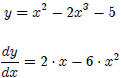
Note: The derivative of a constant is zero .
3. Product Rule
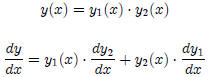
Note: The hi-ho rule can be used as an aid. The
derivative of hi-ho equals,
hi dee ho plus ho dee hi. Here, hi is the function
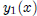, ho is the function
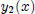
and dee refers to taking the derivative.
Example:
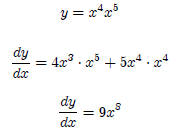
Similarly, using the simple power function example where y = x9, we have:
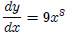
We will be seeing a lot of functions where there maybe two
different variables,
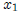and 
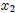, for example 
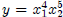: Here, we will not be
able to use the simple
power function rule as adding 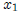and
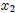is like
adding apples and oranges.
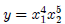
So now we take the derivatives with respect to 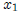and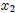
separately, and for
each case we treat the other variable as a constant
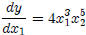, where 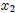is a constant
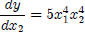, where 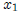is a constant
4. Quotient Rule
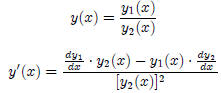
Note: In alot of instances you will encounter y'(x): This
is used instead of
Example 1:
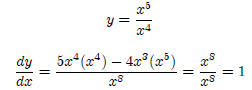
Example 2:
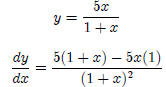
5. Chain Rule
For example if we have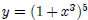 
: Here, we will need to introduce a new
variable, z:
So,
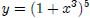,where
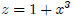
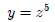
Using the simple power function rule, we obtain
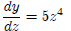
Using the rule for sums :
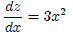
We have the derivative of y w.r.t z, and the derivative of z w.r.t x:
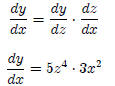
Substituting for z, we get
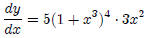
6. Logarithmic Functions
We have a simple logarithmic function y = ln x. The derivative,
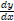, is equal
to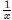 
:(This can be considered as the derivative
of x divided by x )
Example 1:
y = ln 2x,then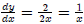 
: (The derivative of 2x
divided by 2x)
Example 2:
y = ln x2, then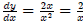 
:(The derivative of
x2
divided by x2)
7. Solving Linear Equations
Economics requires solving systems of linear equations with unknown vari-
ables.
For example, if we have the following system of linear equations:
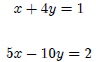
Equating x in terms of y : (You can also try the reverse)
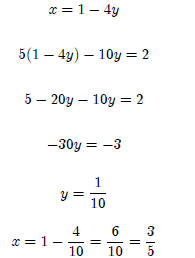
To check our answers, input the two values into the system
of linear equa-
tions:
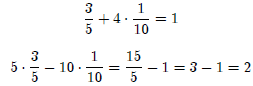
Remember, calculus makes economics easier, not harder.
Once you master
the concepts, you will realize how much fun economics can actually be.
8. Some Practice Questions:
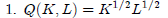
Differentiate Q (K,L) with respect to K and L.
Answer:
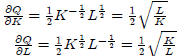
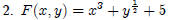
Differentiate F(x, y) with respect to x and y:
Answer:
We will be covering pro…t maximization and cost
minimization problems in
the course. Although, there are many ways to solve them, one of the most useful
tool is the Lagrange multiplier. Use the note below as a guide to help you solve
the problems.
A note on using Lagrange Multiplier
Maximize the utility function, U(x, y) = xy subject to a budget constraint
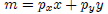
Using Lagrange multiplier, we can write the utility maximization problem
as follows:
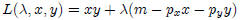
x and y are quantities of goods,
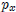is the price of good
x, and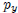 
is the price
of good y, and m is the income level, and λ is the marginal utility of income.
In order to find our first order conditions, we would differentiate with respect
to x, y and λ and then solve the equations to obtain the utility maximizing
quantities of x and y:
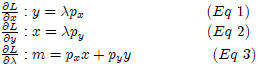
Now substituting for λ, we can use from the first equation
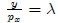and plug
into the second equation to get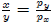 
Substituting x of equation 3 with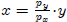 
, we can
get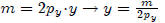 
and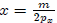 
:
Thus our utility maximization bundle is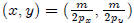 
:
Practice Problem:
Maximize utility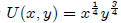 
subject to the following
budget constraint
constraint: 400 - 4x - 4y
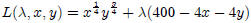
First order conditions:
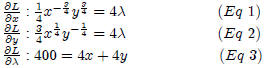
Substituting for λ we get:
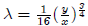
Input the equation for λ into the 2nd equation: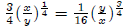
We get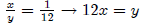 
Now inputting into our 3rd equation, (the budget constraint)
We get 52x = 400
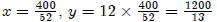
To check our answer: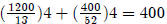 
So we maximize our utility with the following bundle of good x and y:
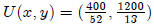
Good luck and welcome to Econ 100A
Prepared by: Aadil Nakhoda
| Prev | Next |