Flying in the wind
An ill wind
You’ve probably heard the expression “Any wind is an ill wind”. When it
comes to flying, that isn’t true if the wind happens to be a tailwind for your
trip.
However, it is true if you are talking about flying a closed course.
Specifically,
if the wind has constant speed and direction and you fly a closed course at a
constant airspeed, your best possible time around the course is when the wind
is calm.
Description
We will assume that the course the airplane flies can be considered as a
simple closed curve in the xy plane and that the speed of the airplane is
greater
than that of the wind. Otherwise, of course, the plane couldn’t negotiate the
course. To negotiate a course in the wind, the pilot must “crab” the airplane
to account for the effects of the wind and remain on course. Part of the time
the wind may be at his tail, increasing his speed over the ground, and part of
the time he is heading into the wind, decreasing his ground speed. We want to
show that the time taken to traverse the course is least when there is no wind.
Analysis
We will be using a bit of vector calculus in what follows.
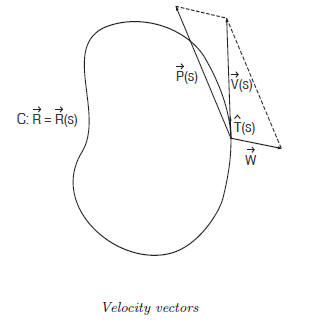
Refer to the above figure. The curve C represents the closed course and is
parameterized by arc length s:
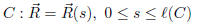
where
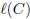represents the length of C. The velocity vector for the airplane is
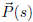with constant length
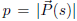representing the airplane’s speed. The
wind is represented by the constant vector
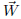with length
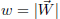representing
the speed of the wind. Note that while the wind is represented by a constant
vector, the airplane’s velocity vector depends on its position s along the curve
because its direction changes . Finally, the vector sum of the wind and airplane
vectors gives the ground velocity vector
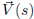whose length
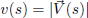represents
the speed along the ground. We need to compute the time to traverse the
course in the wind, which is given by
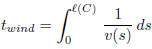
and show that this time is always at least as long as the time it would take
to
traverse the curve C with no wind at the constant speed p of the airplane, which
is
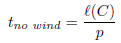
The pilot of the airplane continuously adjusts his heading so that the ground
velocity vector is tangent to the curve C. If we let
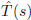be the unit vector tangent
to the curve, then the ground velocity is
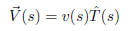
We calculate the ground velocity by adding the wind and airplane velocities:
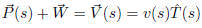
Solving this equation for
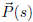gives
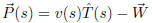
To calculate v (s) we take the dot product of this equation with itself
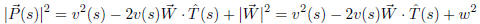
which gives a quadratic equation for v(s).
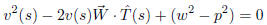
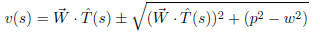
from which we may drop the minus choice which would give a negative value
for v(s).
The equation for t wind becomes
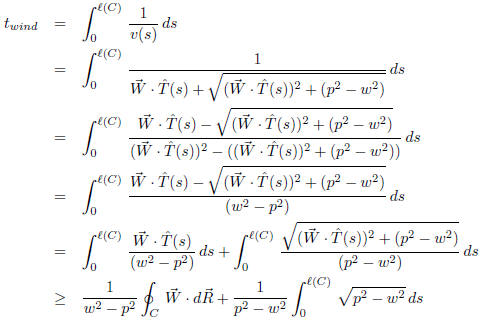
The line integral in the first term is 0 because the
constant vector field
is
conservative. So we have
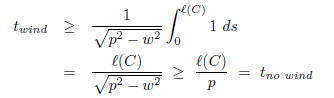
which completes the argument.
| Prev | Next |