Introduction to Mathematical Modeling
Textbook: Explorations In College Algebra, 4th
Edition, by Kime, Clark and Michael, John Wiley & Sons.
ISBN: 9780470281482. The 4th
Edition comes with a code for WileyPlus
registration which is needed.
Note: This course syllabus provides a general plan for the
course; deviations may be necessary.
1. COURSE DESCRIPTION. Mathematical modeling uses graphical, numerical,
symbolic, and verbal
techniques to describe and explore real -world data and
phenomena. Emphasis is on the use of elementary
functions to investigate and
analyze applied problems and questions, on the use of appropriate supporting
technology, and on the effective communication of quantitative concepts and
results. THIS COURSE IS
NOT AN APPROPRIATE PREREQUISITE FOR PRECALCULUS OR
CALCULUS. Students who must
take precalculus must understand the implications of
taking MATH 1101 (See the instructor immediately if
you have any questions).
2. PREREQUISITE. Knowledge of high school algebra II, or equivalent. This
includes algebraic
expressions, first degree equations and inequalities,
exponents, radicals, solving and graphing linear
equations, factoring quadratic
expressions, and other topics.
3. COURSE OBJECTIVES.
Algebra . Students will demonstrate the ability to:
a. Graph points.
b. Graph linear, piecewise linear, exponential, logarithmic, and quadratic
equations and
functions. and identify horizontal asymptotes.
c. Determine the equation of a line given two points or one point and the slope .
d. Determine the absolute value of a quantity.
e. Solve and estimate solutions to linear, quadratic, exponential, and
logarithmic equations,
including use of the properties of exponents and common
and natural logarithms.
f. Solve linear systems of two equations by substitution and elimination ,
including systems
that have a unique solution, no solution, or many solutions.
g. Simplify expressions using the laws of exponents and logarithms.
h. Calculate average rate of change of any function.
i. Perform arithmetic calculations to answer questions regarding two-variable
data
presented in tabular, graphical, or equation form.
j. Express and compare very large and very small numbers using scientific
notation and
orders of magnitude.
k. Factor quadratic expressions.
l. Complete the square of quadratic expressions.
m. Express the square root of negative numbers in terms of
the imaginary unit, i.
n. Given conversion factors, convert units of measure.
o. Use the quadratic formula to solve quadratic equations
Functions. Students will demonstrate:
a. The understanding of the definitions of function, domain, range, independent
and
dependent variables, and input and output.
b. The ability to determine if tables, graphs, and equations represent
functions.
c. The ability to determine the domain and range of functions as mathematical
abstractions
or in a physical context.
d. The ability to determine from the graph of a function the values of the
independent
variable for which the function increases, decreases, or remains
constant.
Linear and piecewise linear functions. Students will demonstrate the ability to:
a. Determine when two real -world variables are related by a linear or piecewise
linear
function.
b. Calculate, and interpret average rate of change as slope.
c. Model the behavior of two real-world variables that are directly proportional
or are
related by a linear or piecewise linear function using tables, graphs,
equations.
d. Evaluate linear and piecewise linear functions.
e. Use a linear function to approximate the value of a non-linear function.
f. Interpret the intersection of the graphs of linear functions as equilibrium
points.
Exponential Functions. Students will demonstrate the ability to:
a. Determine when two real-world variables are related by an exponential
function.
b. Model the behavior of two real-world variables that are related by an
exponential
function using tables, graphs, equations, or combinations thereof
including such
applications as population growth and decay, radioactive decay,
simple and compound
interest, inflation, the Malthusian dilemma, musical pitch,
and the Rule of 70.
c. Change the base of an exponential function to determine rate of growth/decay,
growth/decay factor, and effective and nominal interest rate.
d. Express continuous growth/decay in terms of the number e.
e. Evaluate exponential functions.
f. Determine the exponential equation model from the table or graphical model.
g. Compare linear to exponential growth.
Logarithmic Functions. Students will demonstrate:
a. The ability to determine when two real-world variables are related by a
logarithmic
function.
b. The ability to model the behavior of two real-world variables that are
related by a
logarithmic function using tables, graphs, equations, or
combinations thereof including
such applications as pH and the decibel system.
c. The understanding of the natural logarithm.
d. The ability to graph logarithmic functions.
Quadratic Functions. Students will demonstrate the ability to:
a. Estimate horizontal intercepts of quadratic functions from their graphs.
b. Determine the horizontal intercepts of quadratic functions in factored form.
c. Determine the vertex, axis of symmetry, and horizontal and vertical
intercepts of
quadratic functions in either the a-b-c or a-h-k forms.
d. Convert quadratic functions from the a-b-c form to the a-h-k form and vice
versa.
e. Determine when two real-world variables are related by
a quadratic function by
calculating the average rate of change of the average
rates of change.
f. Model the behavior of two real-world variables that are related by a
quadratic function
using tables, graphs, equations, or combinations thereof
including such applications as
maximum area for fixed perimeter, minimum
perimeter for fixed area, free fall,
maximum profit, and break-even analysis.
4. COURSE COVERAGE. We will cover the following sections from the text:
Chapter 1  Making Sense of Data and Function (1.1 - 1.5)
Making Sense of Data and Function (1.1 - 1.5)
Chapter 2  Rates of Change and Linear Functions (2.1 - 2.8)
Rates of Change and Linear Functions (2.1 - 2.8)
Chapter 3  When Lines Meet: Linear Systems (3.1 - 3.2, 3.4)
When Lines Meet: Linear Systems (3.1 - 3.2, 3.4)
Chapter 4  The Laws of Exponents and Logarithms: Measuring the Universe (4.1 -
4.7)
The Laws of Exponents and Logarithms: Measuring the Universe (4.1 -
4.7)
Chapter 5  Growth and Decay: An Introduction to Exponential Functions (5.1 - 5.6)
Growth and Decay: An Introduction to Exponential Functions (5.1 - 5.6)
Chapter 6  Logarithmic Links: Logarithmic and Exponential Functions (6.1 - 6.5)
Logarithmic Links: Logarithmic and Exponential Functions (6.1 - 6.5)
Chapter 8  Quadratic and Other Polynomial Functions (8.1 - 8.4)
Quadratic and Other Polynomial Functions (8.1 - 8.4)
IMPORTANT NOTE: Georgia State University and its faculty are not responsible for
outcomes due to
individual technical issues, nor scheduled WileyPlus downtimes.
It is expected that the students will be
responsible for completing their work
in a timely fashion as to alleviate any pressures these scheduled
downtimes
occur. All students will be notified of these downtimes by WileyPlus through the
announcements page of the course.
5. COURSE EVALUATION. Your course grade will be determined as follows:
a. Three midterm tests (closed book/notes): 45% (15% each)
b. WileyPlus online homework and quizzes: 20%
c. Excel Projects: 10%
d. Final Exam (closed book/notes, cumulative): 25%
e. Bonus points: For example, the Pre-QL and Post-QL carry bonus points.
Example of Course Grade Computation:
Test Grades: T1 = 88, T2 = 72, T3 = 68; WileyPlus online homework and quizzes =
85;
Excel Project average = 90; 
 Final Exam = 76;
Final Exam = 76;
 Bonus: 1.5.
Bonus: 1.5.
Then the overall course score is 0.15*(88+72+68) + 0.20*85 + 0.10*90 + 0.25*76 +
1.5 = 80.7
6. GRADING SCALE. We will use the following grading scale (C- not available):
 F: Less than 60
F: Less than 60
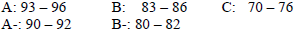
For example, the above score of 80.7 would make a letter
grade of B- for the course.
7. Makeup Policy: No make-up exams will be given unless in some extreme and
documented situations.
Absence from the final exam will result in a grade of F
for the course unless arrangements are made PRIOR
(at least one week before the
final exam) to its administration.
8. CALCULATOR Policy. You are recommended to have a scientific calculator or a
graphing calculator.
If you are not strong in mathematics, I strongly recommend
you obtain a graphing calculator. You are not
allowed to share calculator with
any other party in your class during any in class quiz or exam, unless
permitted
by your instructor.
9. Academic assistance at GSU:
1. Attend academic assistance session, MW 12:00-1:15pm, 120 Kell Hall.
2. Visit the Math Assistance Complex (MAC), Kell Hall 122 (phone: 404-413-6462).
3. Visit the Counseling Center for Learning assistance,
Test anxiety classes, and Student support
services (phone: 404-413-1641)
4. African American Student Services (phone: 404-413-1530)
5. A private tutor list is available at Math Assistance Complex and Math
Department
10. ACADEMIC HONESTY: Cheating/plagiarism will not be tolerated on any work. A
first occurrence
will result in a grade of 0 on the assignment for all concerned
parties as well as an Academic Dishonesty
form being filed with the Dean of
Students. A second occurrence will result in a grade of F for the course
for the
concerned parties and a second Academic Dishonesty form being filed. During
in-class quizzes,
tests, and the final exam you will be instructed to do your
own work, talk to nobody, and not share
calculators. Violations of these
instructions constitute dishonesty and will be handled in accordance with
University policy. The instructor has the option of withholding or denying
credit for answers not
adequately supported by you.
11. Inclement Weather Policy: If the University is closed due to inclement
weather, any exam that may
have been scheduled for that date will be
administered on the next available class date. If an assignment is
due that day
it will be due the next class.
12. Attendance Policy: Attending class is of utmost importance and is your
responsibility and yours alone.
(Attendance will be taken daily). During class
the instructor can clarify important or complex points for
you, observe you
working problems, and answer your questions. However, much, and perhaps most, of
what you learn during the course will occur outside of class; approximately two
hours preparation for each
hour in class over is the norm.
13. Conduct Policy: Turn off all pagers and cell phones before entering the
classroom – having these
items “go off” in class is considered disruptive
behavior and can result in your being administratively
dropped from the course.
In fact, any type of inappropriate conduct may result in your being
administratively dropped from the course.
14. Withdrawal Policy: You cannot withdraw from the course simply by ceasing to
attend class; you must
formally withdraw. If you intend to withdraw, do so
before midpoint (Thursday, October 15th) to be able
to possibly avoid a grade of
“F” or “WF.” If you do not attend class during the first two weeks you will
be
administratively withdrawn.
15. ASSIGNMENTS. Although we will basically follow the attached schedule,
deviations might be
necessary. I will assume that you have read the
corresponding lesson prior to arriving in class and do the
homework assignments
posted on the ULEARN after attending class.
16. EXAM DATES. The dates of the 3 tests are tentative. Make-up tests may be
granted only for extreme
emergencies (such as medical emergencies) that must be
documented.
| Test 1: | Thursday, September 10th, 1:00 – 2:15pm | In class | Chapter 1, 2 |
| Test 2: | Tuesday, October 20th, 1:00 – 2:15pm | In class | Chapter 3, 4, 5 |
| Test 3: | Thursday, November 19th, 1:00 – 2:15pm | In class | Chapter 6, 8 |
| Final Exam: | Thursday, December 8th, 12:30 – 2:30pm | 625 GCB | Cumulative |
17. OTHER IMPORTANT DATES.
Last day to drop a class with full refund: Friday, August 21.
Last day to withdraw from term length classes and possibly receive a W: Thursday, October 15.
Welcome aboard!
| Prev | Next |