LEONHARD EULER

Euler\'s algebra

The impossibility of finding a solution in integers of the equation

x⁴ + y⁴ = z⁴

or even of the equation

x⁴ + y⁴ = z²

was established by Fermat. It appears to have been Euler who in his textbook
Algebra, published in 1770, first established the impossibility of solving the
equation

x³ + y³ = z³:

It is reported in a standard history that he obtained his proof sometime
between 1753 and the time of publication. There is a gap in his proof that
was filled by Legendre and to which we shall return. In essence, it can only
be filled by understanding the decomposition into primes of numbers in Z ( α ).

I observe in passing that Euler\'s algebra was a widely used textbook
for some time. There is still much to recommend it today to the intelligent
amateur. I like to imagine Clausewitz, who began the study of mathematics
as a diversion after being taken pris oner by Napoleon \'s troops during the
battle of Jena, working through a copy of Algebra. He writes to his fiance of
his studies, but unfortunately does not indicate what books he is using.

Euler\'s book starts at the beginning, and even has problems in what is
presently a very hot topic, financial mathematics. I give two examples .

§II.1.36) Ich habe einige Ellen Tuch gekauft und jede 5 Ellen 7 Rthlr.
bezahlt, davon wieder 7 Ellen 11 Rhtlr. verkauft und dabei 100 Rthlr.
gewonnen. Wie viel Tuch ist es gewesen?

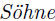§II.1.26) Ein Mann 11000 Rthlr. seine Witwe, zwei   und
drei 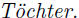Nach seinem Testamente soll die Frau zweimal mehr bekommen
als ein Sohn, und ein Sohn zweimal mehr als eine Tochter. Wie viel bekommt
jeder Erbe?

Corrections and elaborations

There are a number of statements on the previous page that I have taken
from various sources and that are doubtful, as is made clear by an examination
of Weil\'s book on the history of the theory of numbers. First of all, Weil
explains why there is good reason to believe that Fermat had not merely
stated but in fact proved the impossibility of the equation

x³ + y³ = z³, xyz ≠ 0;

in integers. The proof, however, is not extant, the first extant proof being due
to Euler. Moreover, although Euler is a little careless in his Algebra about
the matter, the "gap" in his proof is filled by theorems that he had already
proved and published in 1759. A complete proof does appear in Legendre\'s
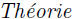des nombres published in 1798. This may be the source of the error.

I shall give two apparently different proofs of the impossibility of this
equation. In essence they are the same. One is that of Euler (and perhaps
also that of Fermat). The other is modelled on later, more general, methods
of Kummer and is meant as an aid to the understanding of his arguments.

These problems appear about half-way through the textbook. By the
end, he has arrived at Fermat\'s theorem for cubes. In between (§II.2.188),
he asks and partially answers when an expression ax ² + cy² is a cube. He
suggests setting

(A)

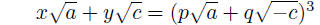
and

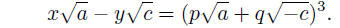
This makes

(B)

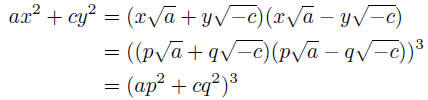
If we expand the left side of (A), we obtain

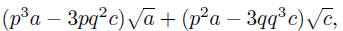
so that (A) can be interpreted as the pair of equations,

(C) x = p³a − 3pq²c, y = 3p²aq − q³c.

Thus these values for x and y ensure that ax²+cy² is a cube. Euler does not,
however, show that, conversely, if ax² + cy² is a cube then integers p and q
can be found that satisfy (C). None the less he uses this converse statement in
his proof of Fermat\'s theorem for the prime 3. So his argument is incomplete.
I present it nevertheless, completing it later.

It appears in the very last chapter of the very last section of the very
last part of the book, in the section entitled, von der unbestimmten Analytik,
which seems to be the late eighteenth, early nineteenth century term for the
search for integral solutions to equations whose solutions are not uniquely
determined. In the last chapter, the problem is to find two integers x and
y such that the sum of their cubes is again a cube, thus to solve Fermat\'s
equation

x³ + y³ = z³.

Now Euler has already introduced in this section some techniques for
solving such equations. I give examples that illustrate Euler\'s expository
style and that illustrate as well some of the principal achievements of number
theory before the appearance of Gauss. All of this material remained after
Gauss and remains today a basic and integral part of the theory of numbers.

In §II.2.41 he asks when a rational number x can be found such that the
rational number x²+1 is a square . He observes that this is certainly possible.
For example, is x = 3/4 then

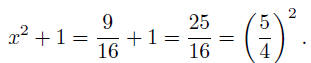
This is of course familiar to us as

3² + 4² = 5²,

because 3 and 4 are two sides of a right-angles triangle whose hypotenuse is
5. So we are meeting the pythagorean theorem again, and of course Fermat\'s
theorem as well, but in the case n = 2 in which solutions are possible.

Euler\'s Algebra offers two methods of solution , of which I present the
first. One sets

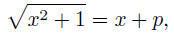
and tries to find p, or rather x and p. Squaring, we obtain

x² + 1 = x² + 2xp + p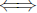² 1 = 2xp + p².

The second equation yields

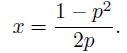
Thus if p = m/n,

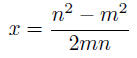
and

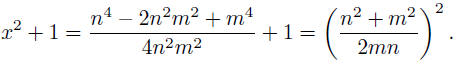
Euler gives a brief list of possibilities

n	2	3	3	4	4	5	5	5	5
m	1	1	2	1	3	1	2	3	4
x

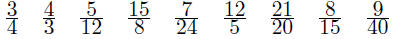He also observes that the solution leads to an in finite number of pythagor-ean
triangles, thus to an in finite number of integral solutions of the equation

p² + q² = r²:

He just takes

p = 2mn, q = n² −m², r= n² +m².

There several other equations whose integral solutions Euler discusses.
Although not immediately pertinent to us, it is worthwhile to spend a little
time with them. He deals with Pell\'s equation, which will reappear in exacerbated
form as the theory of units when we return to Kummer and his
treatment of Fermat\'s equation. He also deals with the search for rational
solutions of certain equations which, in modern termino logy , is the search for
rational points on elliptic curves. Since the Taniyama-Shimura-Weil conjecture,
about which a number of you are curious, often provides, among other
things, an effective method for establishing the existence of such points, Euler\'s
chapters may serve as an introduction not to the modern statements
themselves but to their meaning and purpose.