Math 1113 Final Exam Review
Section 4
For problems 1-3 you are given the rate of rotation of a wheel as well as its
radius.
In each case, determine the following:
a. the angular speed, in units of radians/sec.
b. the linear speed , in units of cm/sec, of a point on the circumference of the
wheel
1. 6 revolutions/sec; r = 12 cm ans: a. 12π rad/sec b. 144π
cm/sec
2. 1080° /sec; r = 25 cm ans: a. 6π rad/sec b. 150π
cm/sec
3. 500 rpm; r = 45 cm ans: a.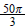 
rad/sec b. 750π
cm/sec
4. Find the values of the six trigonometric functions of the angle in
standard position with the terminal side passing through the point (1, −3).
ans: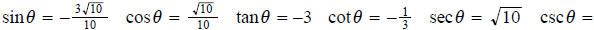 
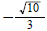
5. If θ is an acute angle in standard position and sinθ = 3/5
, find secθ .
ans: 5/4
6. Find amplitude and period of the function
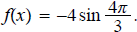
ans: amp = 4, period = 3/2
7. Determine an equation for a cosine curve that has amplitude of 3, period
of π, and phase shift of π/4 to the left.
ans: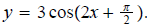
8. Determine an equation for a sine curve that has amplitude of 2, period
of 2, and phase shift of 2/3
to the right.
ans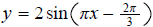
9. Given that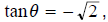 
sinθ > 0; find secθ
.
ans: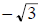 
10. A tree casts a shadow of 8.55 ft when the angle of elevation of the sun
is 55.3°. Find the height of the tree.
ans: 12.3 feet
11. Find x- intercepts of each trigonometric function in the speciffied interval.
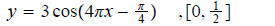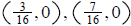
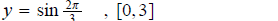ans: 
ans: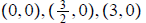 
12. Find exact value of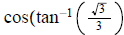 
ans:
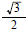
13. Find exact value of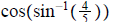 
ans: 3/5
14. Find exact value of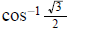 
ans:
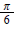
15. Find horizontal asymptote of
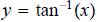[look this up in your notes]
Section 5
Verify the following identities (# 1 - 3).
1.
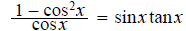
2. (sin x + cos x)(csc x − sec x) = cot x − tan x
3.
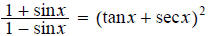
Simplify (# 4 - 6).
4.
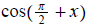ans: − sin x
5.
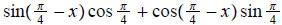
ans: cos x
6.
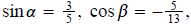α and
β are in quadrant II; find
.
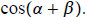ans:− 16/65
Verify each identity (#7 -8).
7.
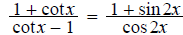
8.
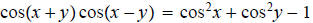
Find all solutions of each equation in the interval 0,2.
9. tan x − 2tanx cos x = 0
ans:
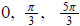
10. 2cos2x − cos x = 1
ans: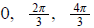
11. 2sec3x + sec2x − 8secx − 4 = 0
ans:
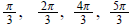
Find all solutions of each equation in the interval
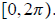
12. tan2x = 3sec2x − 2
ans: No solution
13. cos2x − 3sinx + 2sin2x = 0
ans: 22.5°, 157.5°
14. cos x + 3 = 0
ans: No solution
15.
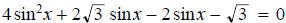
ans: 30°,150°,240°,300°
Section 6
Solve each triangle (#1 - 5).
1. a = 24, b = 32, c = 28
ans:C ≈ 58° A ≈ 47° B = 76°
2. b = 102, c = 150, A = 82°
ans: a ≈ 169 B = 37° C = 61°
3. C = 55°, c = 80, b = 110
ans:No triangle is formed, as sinB ≈ 1.1263
4. B = 25°, C = 40°, c = 40
ans:A = 115° a ≈ 56 b ≈ 26
5. A = 37°, c = 40, a = 28
ans: C = 59°, B = 84°, b = 46 or C = 121°, B = 22°, b = 17
6. Find the components of a vector whose initial and terminal points are
.
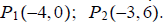ans: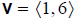 
7. Find the magnitude and direction of the vector
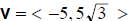
ans: magnitude = 10, direction = 120°
8. Find the magnitude and direction of z = 2 − 3i.
ans: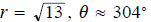
9. Write the complex number z = 5 (cos315° + i sin315°) in standard form.
ans: z ≈ 3.54 − 3.54i
10. Find the vertices and asymptotes of the hyperbola
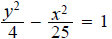
ans: vertices – (0,2), (0, −2)
asymptotes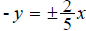
11. Find the vertices of the ellipse
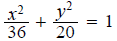
ans: (−6,0), (6,0)
12. Find the 30th term of the sequence
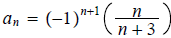
ans: − 10/11
| Prev | Next |