Math 120 Quiz
Directions: Follow all directions carefully. Show all work
(where applicable). Problems without work may
not receive full credit. The quadratic formula is something that you will need
to have memorized. For now,
I will give it to you but will not tell you how to use it. The quadratic formula
is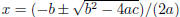 
.
The total number of points on this quiz is 25.
1. Jacob "donates" plasma twice a week. He gets $20 for the first donation and $40
for the second donation
each week. He drives a car that gets 22 miles per gallon and the price of gas is
$3.00. Answer the
following:
(a) (2 points) How much does he get for donating over a four week period?
So each week he gets $20+$40=60. Over four weeks he gets 4 · 60 = 240. So $240.
(b) (4 points) Suppose the place he donates is 45 miles away. How many gallons
of gas must he use for
each trip? How much does the gas cost him per trip?
His car gets 22 miles per gallon, so 22x = 45,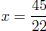 
, x
≈ 2.045455. So about 2.0454545 gallons are
used one way. So for the trip he would need 2 · 2.0454545 ≈ 4.0909 gallons per trip.
Gas is $3 a gallon, so 3 · 4.0909 ≈ 12.27. So it costs him $12.27 or, more
accurately $12.28. (Here
we would want to round up even though there is a two following the seven. The
reason being that
we do not have parts of cents and the gas station will round up).
(c) (4 points) What is Jacob's total pro t for a four week period?
This was tricky. Firstly it cost him $12.28 per trip. He makes two trips a week,
so each week it
costs him $24.56 to drive there and back. Over four weeks, we take 4 · 24.56 =
98.24. So it costs him
$98.24 in gas money. He makes $240 (from part (a)), so his pro t is
$240-98.24=141.76 or $141.76.
2. Solve the following linear equations .
(a) (2 points) -17y + 12 = 3y + 4
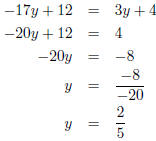
(b) (3 points)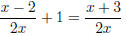 
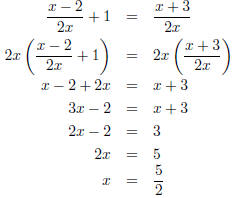
I noted on some of your papers that I do not like mixed
numbers (i.e. writing your final solution as
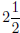). This is a personal preference , but as you
go on in mathematics it is easier and easier to mess
up if you write an improper fraction as a mixed number.
3. Perform the indicated operations involving complex numbers and write the
result in standard form.
(a) (2 points) (7 + 2i)(15 - i) Here we need to foil.
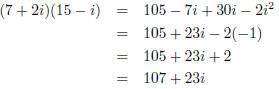
(b) (3 points)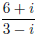 
Here we must multiply by one in a clever way. We use the complex conjugate 3 + i over itself.
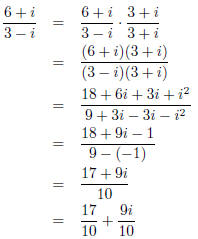
4. Given the following quadratic equation x 2 + 4x + 12 = 0
do the following:
(a) (1 point) Find the discriminant of the quadratic.
The discriminant of a quadratic equation is the b 2 - 4ac part of the quadratic
equation. Here we
have a = 1, b = 4, c = 12 so we look at 42 - 4(1)(12) = 16 - 48 = -32. So the discriminant of this
quadratic is -32.
(b) (1 point) What does the discriminant tell you about the solutions to the
quadratic equation?
Here, as -32 < 0, we know that we will get two (distinct) complex solutions.
(c) (3 points) Solve the quadratic equation.
We simply apply the quadratic formula.
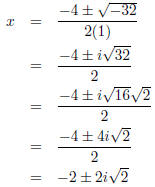
| Prev | Next |