Math 172-1 Final Exam Review Sheet

The final exam covers sections 5.6, 5.7, chapters 6, 7, 8, 10, and 11. No graphing /symbolic
calculators allowed and no notes are allowed. You may bring a simple scientific calculator.
Don't be late. Bring photo ID.

Chapter 5: Integration

6. Substitution and Area Between Curves: Be able to use substitution to calculate
definite integrals. Be familiar with integrals of symmetric functions. Be able to find the
area between two curves. Note that we can do this using either the usual vertical strips or
horizontal strips.

7. The Logarithm Defined as an Integral: Be able to evaluate integrals that result
into logarithmic terms. Be able to evaluate integrals of exponential functions of any base.

Chapter 6: Applications of Definite Integrals

1. Volumes by Slicing and Rotation About an Axis: Be able to find the volume of
a solid be integrating cross-sections. Know how to find the area of a cross section. What is a
solid of revolution. Be familiar with the disk method. Be familiar with the washer method.
Be prepared for any axis of revolution.
2. Volumes by Cylindrical Shells: Be able to use the shell method to find the volume
of a solid of revolution. Be prepared for any axis of revolution.
3. Lengths of Plane Curves: Be able to find the length of a parametric curve. Be able
to find the length of a function y = f(x). Be able to find the length of a function x = g(y).
4. Areas of Surfaces of Revolution: Be able to find the area of a surface generated
by revolving a curve about either axis.
5. Exponential Change and Separable Differential Equations: Be able to derive
the exponential change function for a differential equation. Be able to solve a separable
differential equation. Be able to find both the general and a particular solution to a differ-
ential equation. Be able to show that a given function is indeed a solution to a differential
equation.
6. Work: Be familiar with Hooke's Law. Be able to find the spring constant. Be able
to find the work to compress or stretch springs. Be able to find the work to move objects
along a straight line. Be able to find the work required to empty an object of liquid.
7. Moments and Centers of Mass: Be familiar with torque, moments, mass, and
center of mass. Given a two-dimensional region, be able to find the object's moment about
either the x or y axis, the object's mass, and the coordinates of its center of mass. You may
need to use the either vertical or horizontal strips.

Chapter 7: Techniques of Integration

1. Integration by Parts: Be familiar with the integration by parts formula. Be able
to evaluate both definite and indefinite integrals with exponential terms, logarithmic terms,
and trigonometric terms. What is we have something like 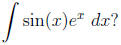What about the
reduction formulas?
2. Trigonometric Integrals: Be able to evaluate integrals with powers of sin(x) and/or
cos(x), with powers of tan (x) and/or sec(x), products of sines and cosines, and square roots
of terms involving trig functions. Know your trig identities, page 26 and 27.
3. Trigonometric Substitutions: Be able to convert integrals involving square roots
and other rational exponents into trigonometric integrals. Know the Pythagorean Theorem.
Be able to draw the appropriate triangle for each type of substitution. Know your trig
identities, page 26 and 27.
4. Integration of Rational Functions by Partial Fractions : Be able to express a
rational expression as a sum of its factors, its partial sum. Does it matter if the factors are
linear or quadratic ? Does it matter if the factors are repeated, i.e. (x - 2)⁴? What if a factor
is a quadratic? Be able to do long division. Be able to find the antiderivative of a rational
function by using partial fractions. What is
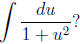
7. Improper Integrals: Be able to determine if a type I improper integral (an integral
with infinite limits of integration) converges or diverges. Be able to determine if a type
II improper integral (an integral where the integrand is discontinuous (infinite) at a point)
converges or diverges. When does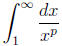 converge and diverge? We talked about three
methods for doing such things: direct calculation, using the direct comparison test, and
using the limit comparison test. Be familiar with these.

Chapter 8: Infinite Sequences and Series

1. Sequences: Be familiar with sequences: notation, identifying patterns, etc. Be able
to determine whether a given sequence converges (and to what) or diverges (and to what).
Be familiar with the algebra of sequences. Be familiar with recursive sequences.
2. Infinite Series: Know what a partial sum is. Know what an infinite series is. Be
super familiar with the geometric series. When does it converge/diverge and to what? Be
able to find the sum of a telescoping series. Be able to use the divergence test. Be familiar
with the algebra of series.
3. The Integral Test: Be able to use the integral test to test for convergence. Is
the resulting integral equal to the sum? Be familiar with the p-series. When do they
converge/diverge? What does the harmonic series do?
4. The Comparison Tests: Be able to use the (direct) comparison test to test for
convergence. Be able to use the limit comparison test to test for convergence.
5. The ratio and Root Tests : Be familiar with both the ratio tests. For some
problems, either test works, but one may be easier to implement then the other. Be prepared
for factorials and n-th powers. You may need to use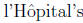 Rule. Remember how to
evaluate infinite limits of ratios.
6. Alternating Series, Absolute and Conditional Convergence: Know what an
alternating series is. Be able to use the alternating series test. Be able to justify the three
conditions. What does the alternating-harmonic series do? Know the difference between
absolute and conditional convergence. Does one imply the other? If so, which one?
7. Power Series: Know what a power series is. Know the basic power series

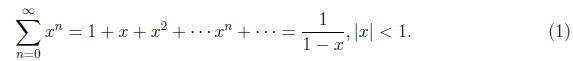
Be able to find the sum of a power series by combining geometric series with substitution.
Be able to find where a power series converges by using either the ratio or root tests. Be
able to find a power series radius and interval of convergence. Be able to both differentiate
and integrate power series.
8. Taylor and Maclaurin Series: Know what Taylor and Maclaurin series are and
how to find them. If given a function with continuous derivatives up to order n, be able to
find its Taylor polynomials up to order n about x = a.
9. Convergence of Taylor Series: Be able to find the interval of convergence of a
Taylor series. Be able to find a Taylor series by using the basic known Taylor series in
combination with some algebra and substitution. Be able to use Taylor series to evaluate
integrals and limits.
Note: Know the Taylor series for
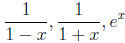, sin(x), cos(x).
10. The Binomial Series: Know what a binomial series is. Be able to compute
combinations. Be able to use the basic form of the binomial series along with substitution
to find other binomial series.

Chapter 10: Vectors and the Geometry of Space

1. Three-Dimensional Coordinate Systems : Know what space is. Be able to both
plot and identify points, simple lines, and simple planes. Be able to identify regions in space.
Know the distance formula. Know what a sphere is, even when not centered at the origin.
2. Vectors: In both the plane and space, know what a vector is. Be able to find the
vector between two points. Be able to sketch vectors. Be able to find the length of a vector.
Know both vector addition and scalar multiplication . Graphically, understand how vector
addition and substraction relate to the sides and diagonal of a parallelogram. Be able to
find unit vectors. Know what the standard unit vectors are. Know the midpoint formula.
Be familiar with vector arithmetic .
3. The Dot Product: Be able to find the dot product. Be able to find the angle
between two vectors. Be able to find angles. What is the dot product is zero? When are two
vectors orthogonal? Know the properties of dot products. Be able to find vector projections.
Be able to find effective force in a given direction. Be able to find work.
4. The Cross Product: Know the definition of the cross product. When are two vectors
parallel? What does a zero cross product tell us? Know the properties of the cross product.
Be able to find the area of a parallelogram. Be able to use determinants to calculate cross
products. Be able to find the area of a triangle by using the cross product. Be able to find
unit normal vectors. Be able to find torque. Be able to use the triple scalar or box product
to find the volume of a parallelpiped.
5. Lines and Vectors in Space: Be able to formulate a line in space. What is needed?
Be able to formulate a plane in space. What is needed?
6. Cylinders and Quadric Surfaces: Know what a cylinder in space is. Be able
to sketch simple ones. Be familiar with the six-quadric surfaces. Know the equations for
ellipsoids , elliptic paraboloids, cones, etc. for various orientations.

Chapter 11: Vector- Valued Functions and Motion in Space

1. Vector Functions and Their Derivatives: Know what vector-valued functions
are. When is one differentiable? How do we find velocity, speed, acceleration, unit tangent
vector, and how do we write velocity as a product of speed and direction?
2. Integrals of Vector Functions: Be able to integrate vector-valued fucntions. Be
able to solve an initial-value problem. Know the ins and outs of ideal projectile motion.
What two values do we use for gravity g?
3. Arc Length in Space: Be able to find arc length in space.
4. Curvature of a Curve: Given a curve in the plane or space, be able to find its
curvature at a point. Be able to find the prncipal unit normal vector of a curve.
5. Tangential and Normal Componets of Acceleration: If given a curve, be able
to find tangential and normal scalar components of acceleration without finding T and N.
Be able to find the binormal vector. Should torsion be bonus?

Look over this list and the sample exams. Don't study material that we haven't covered
or not on the list. Then bring questions regarding those to the review.