Math Homework

Problem 1: (15 points)
Consider the Boolean algebra (B,+, *,' , 0, 1) represented by this Hasse diagram:

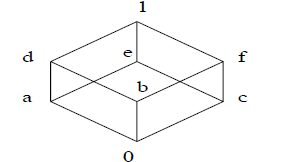
Give the tables of +, *, and '.

Problem 2: (2' points)
For any integer n > 1 let D_n be the set of positive divisors of n. Define 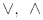, and ' on
D_n by 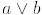= lcm (a, b) (that is, least common multiple of a and b), 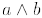= gcd(a, b) (that
is, greatest common divisor of a and b), and a' = n/a. Define in D_n the relation : 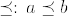if

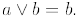
a) Show that 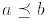if and only if a divides b .
b) Prove that 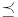is a partial order relation in D_n.
c) Draw the Hasse diagrams of D₄, D₆, D₈ and D₁₀.
d) Which of the following sets is a Boolean algebra : D₄, D₆, D₈ and D₁₀? Explain why.
For each Boolean algebra indicate what its 0 and 1 elements are.

Problem 3: (15 points)
Let 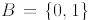be a Boolean algebra and let 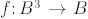be the Boolean function such
that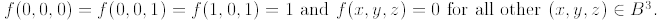
a) Write f in disjunctive normal form and in conjunctive normal form.
b) Give the truth table of f' (the complement of f).
c) Give f' in disjunctive normal form and in conjunctive normal form.

Problem 4: (2' points)
Minimize each of the following Boolean expressions using Karnaugh maps. Show the
Karnaugh maps.

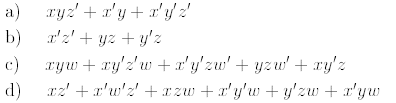
Problem 5: (15 points)
Let f and g be two Boolean functions of x, y, z, w where f(x, y, z,w) = 1 if and only
if at least two of x , y, z, w have value 1, and g(x, y, z,w) = 1 if and only if at most two of
x, y, z, w have value 1.
a) Give the truth tables of f and g.
b) Minimize f and g using Karnaugh maps

Problem 6: (15 points)
Let (B,+, *,' , 0, 1) be a Boolean algebra . Define 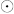as follows:
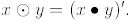
a) Evaluate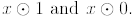
b) Express 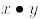using the operation but without using +, *, or '.
c) Express x + y using the operation but without using +, *, or '.