Mathematical Competition

a₁ Let f : R^2 -> R be a function such that f(x, y) +
f(y, z) + f(z, x) = 0 for all real numbers x, y, and z.
Prove that there exists a function g : R -> R such that
f(x, y) = g(x) − g(y) for all real numbers x and y .

a₂ Alan and Barbara play a game in which they ta_ke turns
filling entries of an initially empty 2008 × 2008 array.
Alan plays first. At each turn, a player chooses a real
number and places it in a vacant entry. The game ends
when all the entries are filled. Alan wins if the determinant
of the resulting matrix is nonzero; Barbara wins if
it is zero . Which player has a winning strategy?

a₃ Start with a finite sequence a₁, a₂, . . . , an of positive
integers. If possible, choose two indices j < k such
that a_j does not divide a_k, and replace a_j and a_k by
gcd(a_j , a_k) and lcm(a_j , a_k), respectively. Prove that if
this process is repeated, it must eventually stop and the
final sequence does not depend on the choices made.
(Note: gcd means greatest common divisor and lcm
means least common multiple.)

A4 Define f : R -> R by

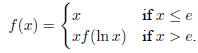
Does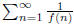 converge

A5 Let n≥3 be an integer. Let f(x) and g(x) be
polynomials with real coefficients such that the points
(f(1), g(1)), (f(2), g(2)), . . . , (f(n), g(n)) in R^2 are
the vertices of a regular n-gon in counterclockwise order .
Prove that at least one of f(x) and g(x) has degree
greater than or equal to n − 1.

A6 Prove that there exists a constant c > 0 such that in every
nontrivial finite group G there exists a sequence of
length at most c ln |G| with the property that each element
of G equals the product of some subsequence.
(The elements of G in the sequence are not required to
be distinct. A subsequence of a sequence is obtained
by selecting some of the terms , not necessarily consecutive,
without reordering them; for example, 4, 4, 2 is a
subsequence of 2, 4, 6, 4, 2, but 2, 2, 4 is not.)

B1 What is the maximum number of rational points that can
lie on a circle in R ^2 whose center is not a rational point?
(A rational point is a point both of whose coordinates
are rational numbers.)

B2 Let 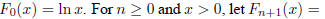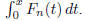Evaluate

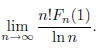
B3 What is the largest possible radius of a circle contained
in a 4-dimensional hypercube of side length 1?

B4 Let p be a prime number. Let h(x) be a
polynomial with integer coefficients such that
h(0), h(1), . . . , h(p^2 − 1) are distinct modulo p^2.
Show that h(0), h(1), . . . , h(p^3 − 1) are distinct
modulo p^3.

B5 Find all continuously differentiable functions f : R ->
R such that for every rational number q, the number
f(q) is rational and has the same denominator as q .
(The denominator of a rational number q is the unique
positive integer b such that q = a/b for some integer a
with gcd(a, b) = 1.) (Note: gcd means greatest common
divisor .)

B6 Let n and k be positive integers. Say that a permutation
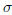of {1, 2, . . . , n} is k-limited if 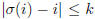for all
i. Prove that the number of k-limited permutations of
{1, 2, . . . , n} is odd if and only if n 0 or 1 (mod
2k + 1).