Mathematical Tools for Economists I
Course description:
This course provides an introduction to fundamental mathematic and statistic
tools, which are
essential to understand economic theories. It is the first course in a
two-course sequence. We
will start with a review of some basic algebraic operations, functions and
graphs . Next we
will cover financial mathematics, matrices, and linear programming. Finally a
basic
probability theory will be presented.
Materials:
Required:
Essentials of College Mathematics, 3 rd edition,
by Raymond A. Barnett and Michael R. Ziegler.
Optional:
Student Solutions Manual for
Essentials of College Mathematics, 3rd edition.
A scientific calculator is required for this course. Although no particular
model is required,
the ones that can handle the calculation of net present value , annuity, and
future value will be
quite helpful for this class.
Grading:
There will be several take-home quizzes, in-class extra credits, three midterm
exams, and a
compulsory cumulative final exam. Your course grades will be determined
as followings:
Take-home quizzes and in-class extra credits 15 points
Midterm Exam 1 
25 points
Midterm Exam 2 25 points
Midterm Exam 3 25 points
Final 
35 points
Take-home quizzes are designed to help you learn how to solve mathematical
problems and
familiarize yourself with math tools needed to solve them. You are also
encouraged to work
on problem sets in the textbook.
There will be absolutely no make-up exams. The Final cannot be replaced with any
other
exam under any circumstances. Only two midterm exams will be counted toward your
final
grade; the midterm exam with the lowest score will be dropped. Your grade will
be
assigned based on the following scale
| Average Points |
 |
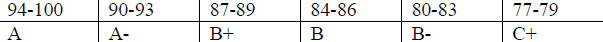| Grade | |
| Average Points |
 |
| Grade |
General Policies
You should come and talk to me in my office hours if you have any questions
about the class.
Additional office hours can be arranged if necessary. Write me e-mail if you
want to make
appointment.
Disabilities and University policies
The Economics Department will make reasonable accommodations for people with
disabilities. For more information, see the web page of the Office of Disability
Services.
We will make reasonable accommodations for students who have conflicts between
religious
observance dates and course examinations or assignments. Please talk to me at
the beginning
of the semester, if you think you may require such accommodation.
Tentative Schedule
Tentative schedule for midterm exams and final exam is following:
Midterm1: 
February 16, 2003
Midterm2: March 12, 2003
Midterm3: April 14, 2003
Final exam: 
May 3, 2004 : 1.30-3.30 p.m.
This schedule is subject to change if necessary .
| Week | Date | Topic |
| 1 | 01/12-01/14 | Introduction 1-1 Sets |
| 01/16 | 1-2 Algebra and real numbers | |
| 2 | 01/19 | Martin Luther King, Jr. Day ( No class) |
| 01/21 | 1-3 Basic operations on polynomials | |
| 01/23 | 1-4 Factoring polynomials | |
| 3 | 01/26 | 1-5 Basic operations on rational expressions |
| 01/28 | 1-6 Integer exponents and square root radicals | |
| 01/30 | 1-7 Rational exponents and radicals | |
| 4 | 02/02 | 2-1 Linear equations and inequalities in one variables |
| 02/04 | 2-2 Quadratic equations | |
| 02/06 | 2-3 Cartesian coordinate system and straight lines | |
| 5 | 02/09 | 2-4 Functions |
| 02/11 | 2-5 Linear and quadratic functions | |
| 02/13 | Review | |
| 6 | 02/16 | Midterm Exam 1 |
| 02/18 | 3-1 Exponential functions | |
| 02/20 | 3-2 The exponential function with base e | |
| 7 | 02/23 | 3-3 Logarithmic function |
| 02/25 | 4-1 Simple interest | |
| 02/27 | 4-2 Compound interest | |
| 8 | 03/01-03/03 | 4-3 Future value of an annuity : sinking funds |
| 03/05- | 4-4 Present value of an annuity: amortization | |
| 9 | 03/08 | |
| 03/10 | Review | |
| 03/12 | Midterm Exam 2 | |
| 10 | 03/15 | 5-1 Systems of linear equations in two variables |
| 03/17 | 5-2 Systems of linear equations and augmented matrices | |
| 03/19 | 5-3 Gauss- Jordan Elimination | |
| 11 | 03/22-03/26 | Spring Break ( No class) |
| 12 | 03/29 | 5-4 Matrices-Addition and Multiplication by a number |
| 03/31 | 5-5 Matrix multiplication | |
| 04/02 | 5-6 Inverse of a square matrix | |
| 13 | 04/05 | 5-7 Matrix equations and systems of linear equations |
| 04/07 | 6-1 Systems of linear inequalities in two variables | |
| 04/09 | 6-2 Linear programming in two dimensions | |
| 14 | 04/12 | Review |
| 04/14 | Midterm Exam 3 | |
| 04/16 | 7-1 Basic counting principles | |
| 15 | 04/19 | 7-2 Permutations and Combin |
| 04/21 | 7-3 Sample spaces and events | |
| 04/23 | 7-4 Empirical probability | |
| 16 | 7-5 Random variable, probability distribution, and | |
| 04/26 | Expectation | |
| 04/28 | Review | |
| 04/30 | Review |
| Prev | Next |