Matlab and Numerical Approximation

ASSIGNMENT 1

1. Enter the matrices

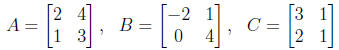
and carry out the following:

(a) Verify that (A + B) + C = A + (B + C).
(b) Verify that (AB)C = A(BC).
(c) Verify that A(B + C) = AB + AC.
(d) Decide whether AB is equal to BA.
(e) Find (A + B)², (A² + 2AB + B²) and
(A² + AB + BA + B²).
(f) Find A² - B², (A - B)(A + B) and
(A² + AB - BA + B²).

2. Enter

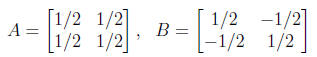
and do the following:

(a) Compute A², A³, etc. Can you say what Aⁿ will be? Explain why this is true.

(b) Compute B², Can you explain why this is true. What does this tell you about
matrix multiplication that is different from squaring numbers ?

(c) Find AB and BA. What do you learn from this that is not true for multiplication
of numbers ? (hint: if a is a real number and a² = 0, then a = 0).

3. Find the inverse of the matrices (if they exist) and check that the result is correct by
multiplying the matrix times its inverse.

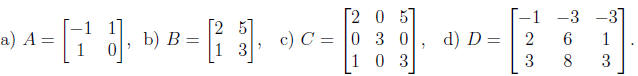
4. Generate an 8 × 8 matrix and an 8 × 1 vector with integer entries by

A = round(10 * rand(8)); b= round(10 * rand(8; 1));

(a) Use °ops to count the number of floating point operations needed to solve Ax = b
using the \ notation.

(b) Reset °ops to zero and resolve the system using the row reduced echleon form of
the augmented matrix [A b] (i.e., U = rref([A b])). The last column of U (call it y)
is the solution to the system Ax = b. Count the °ops needed to obtain this result.

(d) The solutions x and y appear to be the same but if we look at more digits we see
that this is not the case. At the command prompt type format long . Now look at
x and y, e.g., type [x y]. Another way to see this is to type x - y.

(e) which method is more accurate ? To see the answer compute the so-called residuals,
r = b - Ax and s = b - Ay. Which is smaller?

When you are finished reset format to short - format short.

5. Given the matrices

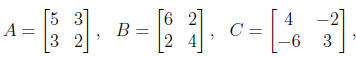
solve the matrix equations:

(a) AX + B = C,
(b) AX + B = X,
(c) XA + B = C,
(d) XA + C = X.

6. Let A = round(10 * rand(6)). Change the sixth column as follows. Set

B=A' % (take the transpose of $A$)

now type

A(:,6)=- sum (B(1:5,:))'

Can you explain what this last command does? Compute

det(A)
rref(A)
rank(A)

Can you explain why A is singular?

7. Let A = round(10*rand(5)) and B = round(10*rand(5)). Compare the following pairs
of numbers.

(a) det(A) and det(A').
(b) det(A + B) and det(A) + det(B).
(c) det(AB) and det(A) det(B).
(d) det(A^-1) and 1/ det(A).

8. Look at help on magic and then compute det(magic(n)) for n = 3;,4, 5, …,10. What
seems to be happening? Check n = 24 and 25 to see if the patterns still holds. By pattern
I mean try to describe in words what seems to be happening to these determinants.