Moving Between Fractions and Decimals
You see decimals every day, in lots of different places .
Can you tell where
each of the decimals below was found?

3.1 Making Smaller Parts
Decimals give us a way to write special fractions
that have denominators
of 10 or 100 or 1,000 or 10,000 or even 100,000,000,000. In Investigation 1,
you folded fraction strips. One of the strips you made was a tenths strip,
shown on the next page.
Getting Ready for Problem 3.1
Suppose you need more marks to show a fraction. Look at the tenths strip.

• How could you fold a tenths strip to get a hundredths
strip?
• How would you label this new fraction strip?
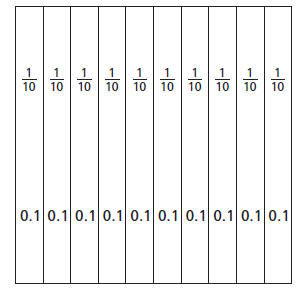
A tenths grid is also divided into ten equal parts. It
resembles a tenths
fraction strip, but it is square. Below is a tenths grid that shows the fraction
and its decimal equivalent represented by each section of the grid.
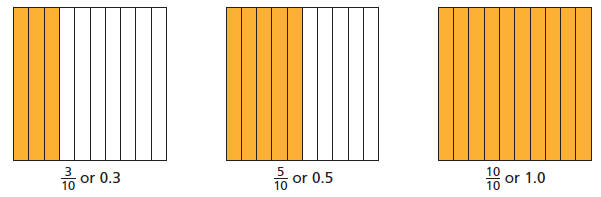
Here are some examples of fractions represented on tenths
grids. The
fraction name and decimal name for the shaded part are given below each
drawing.
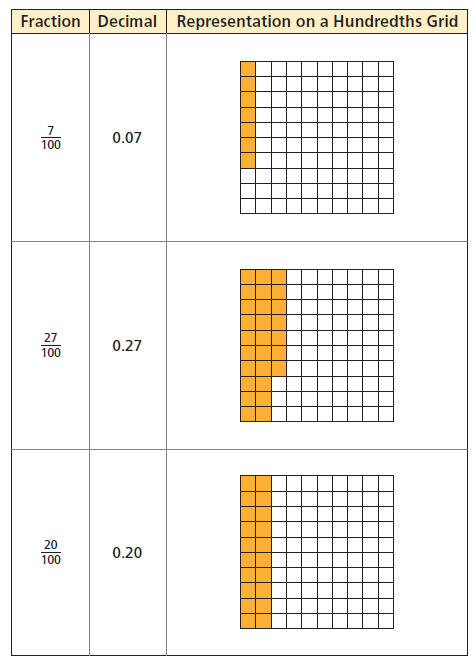
You can further divide a tenths grid by drawing horizontal
lines to make ten
rows. This makes 100 parts. This is called a hundredths grid.

Fractions can also be represented on a hundredths grid.
You can write
fractional parts of 100 as decimal numbers, as in the following examples:
Problem 3.1 Using Tenths and Hundredths
A.
1. Mark and label the fractions 1/4,2/4,3/4,and 4/4 on a hundredths fraction
strip like the one shown .

2. After marking each fraction, shade that fraction on a
hundredths grid like the one at the right.

3. Write a fraction that shows how many hundredths you shaded.
4. Write a decimal that shows how many hundredths you shaded.
B.
1. Which of the fractions could be easily shown on a tenths
grid or a tenths fraction strip?
2. Write number sentences showing equivalent fraction and
decimal forms for each fraction above. Here is an example
that uses the fraction 1/5:
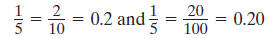
C. Rewrite the fractions below using denominators
of 10 or 100.Then,
write a decimal for each fraction.

D. Lin, a sixth-grader at Pleasant Valley School,
won a giant fruit bar for
selling the most posters in the school fundraiser. The bar is 10 inches
by 10 inches and is marked into 100 square-inch sections. Lin decides
to share her fruit bar with some friends.

1. Lin gives 0.1 of the bar to Bailey. Describe two ways
Lin could cut the bar to share it with Bailey.
2. Lin gives 0.25 of the bar to Lula. Describe two ways
that she could cut the bar to share it with Lula.
3. Lin gives of the bar to her little sister, Donna, who
helped her sell the posters for the fundraiser. Write
two decimals that represent how much of the bar
Donna gets.
4. Lin gives of the bar to Patrick. Write a decimal
that represents how much of the bar Patrick gets.
5. Shade a hundredths grid to show one way that Lin
could cut all of the sections to give to her friends.
6. Who got more of the fruit bar—Bailey, Lula, Donna, or Patrick?
Explain.
7. How much of the bar was left for Lin?
3.2 Making Even Smaller Parts
The place value chart below shows a set of special numbers
in both fraction
and decimal form. Think about these questions as you look at the chart:
What do you notice about the denominators of the fractions as you move to
the right from the decimal point?
Why are these denominators useful in writing fractions as decimals?

Some fractions can be written as decimals using only the tenths place.
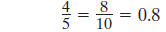
Some fractions, like are difficult to represent with
tenths. You can write 1/4
as an equivalent fraction with a denominator of 100 to find the decimal
representation.
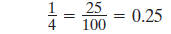
You can think of 1/4 as 25 hundredths or as 2 tenths and 5
hundredths.
For some fractions, you may need to section a grid into even more parts to
represent denominators such as 1,000 or 10,000.
Getting Ready for Problem 3.2
• What might a hundredths grid look like if each square
were subdivided
into 10 equal parts? How many parts would the new grid have?
• What is a fraction name for the smallest part of this new grid? What is
its decimal name?
Problem 3.2 Place Values Greater Than Hundredths

A.
1. What fraction of the grid at the right is shaded?
2. How many hundredths are shaded? Write your
answer as a fraction and as a decimal.
3. If you shaded the same fraction on a thousandths
grid, how many thousandths would be shaded?
Write your answer as a fraction and as a decimal.
B. Write the following sets of fractions as decimals.
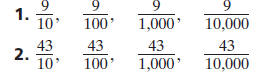
3. What patterns do you see in parts (1) and (2)?
C. Use the following decimals to answer parts (1) and (2).
0.23 0.7011 2.7011 0.00006
1. Write each of the decimal numbers in words.
2. Write each of the decimal numbers as fractions or mixed numbers.
D. For each pair of numbers, find another number that is between them.
1. 0.8 and 0.85 2. 0.72 and 0.73
3. 1.2 and 1.205 4. 0.0213 and 0.0214
5. Describe one strategy that you used to find numbers between
decimals in parts (1)–(4).
3.3 Decimal Benchmarks
Below are representations of 3/4 on a hundredths grid and
on a number
line.
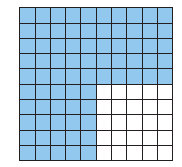
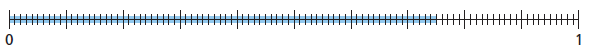
Consider these questions:
Each representation shows that is 75 out of 100 parts. How
would you write this as a decimal?
Different representations are usually good for different
things. Which representation, the grid or the number line,
do you find most useful?
Sometimes knowing a little can go a long way! With
decimals and fractions, knowing just a few fractions and
their decimal equivalents can help you think about many
other fractions and their decimal equivalents. In Problem 3.3
you will make a list of benchmarks that show
equivalent fractions and decimals.
Problem 3.3 Decimal Benchmarks
Mary wants to make a list of decimal benchmarks for these
fraction
benchmarks:
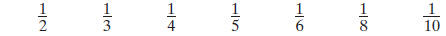
A.
1. For which of Mary’s benchmark fractions do you already know
the decimal equivalent? Show how you know.
2. Use hundredths grids to find decimals that represent or are close
approximations for the ones you do not know.
3. Compare your decimals for 1/4 and 1/8.
4. Compare your decimals for 1/3 and 1/6.
B. Use your work with Mary’s benchmark list to help you find decimal
equivalents for the following groups of fractions:

4. Describe strategies you used to find decimal equivalents
C. Which fraction benchmark is each decimal
nearest?
1. 0.18
2. 0.46
3. 0.225
4. 0.099
5. Describe one strategy that you used to find answers to parts (1)–(4)
Did you know?
Fractions like 1/2,1/4,1/5,and 1/10 all can be represented
easily by decimals.
However, a fraction such as requires careful thinking. It is easy to see that
is between 0.3 and 0.4, and also between 0.33 and 0.34.We could go on
and see that is between 0.333 and 0.334.
Where do we stop and get an exact value? It turns out that
we do not ever
get an exact answer if we stop finding additional decimal places! To write
something like an exact value, we would need to write 1/3 as 0.33333c,
where the “. . .” means that we go on and on, without stopping. When we
need to stop somewhere, we write approximations for fractions. We often
approximate 1/3 by decimals such as 0.33, 0.333, or even 0.3333.We can use as
many 3’s as we need for whatever accuracy is appropriate.
3.4 Moving From Fractions to Decimals
In August 2004, Hurricane Charley swept though Cuba ,
Jamaica, and
Florida. It destroyed many homes and caused lots of damage to land and
buildings. Many people had no place to live and little clothing and food. In
response, people from all over collected clothing, household items, and food
to send to the victims of the hurricane.
One group of students decided to collect food to
distribute to families
whose homes were destroyed. They packed what they collected into boxes
to send to the families. The students had to solve some problems while they
were packing the boxes.

Problem 3.4 Moving From Fractions to Decimals
The students had 14 boxes for packing the food they
collected. They wanted
to share the supplies equally among the 14 families who would receive the
boxes. They had bags and plastic containers to repack items for the
individual boxes. They also had a digital scale that measured in kilograms
or grams. (Remember that 1 kilogram = 1,000 grams.)

A. How much of each item should the students
include in each box?
Explain how you found your answer.
B. One student calculated the amount of powdered
milk by writing 77/14,
then 11/2, or 5.5 kilograms per box. Use this method to calculate the
amount of the other items per box.
C. Another student calculated the amount of Swiss cheese
to include in
each box by entering 10.5 into her calculator and dividing by 14. Is this
a good method? Why or why not?
D. How does this problem suggest a way to change a
fraction to a
decimal? Explain.
3.5 Ordering Decimals
The decimal number system is based on place value. The
value of a digit in
a number depends on the place where it is written. So the “2” in “20” has a
different meaning from the “2” in “0.02.”The chart below shows the place
value for each digit of the number 5,620.301.
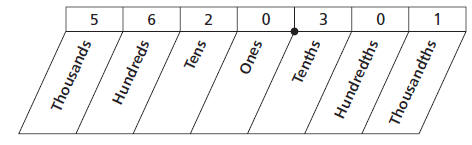
When you read decimal numbers that are greater than one,
you say “and”
to separate the whole number and decimal parts. For 2.5 you say “2 and 5
tenths.”
Getting Ready for Problem 3.5
Consider these numbers:
2 0.2 20 0.00002
• How does place value tell you which number is greatest ?
Decimals can also help you to answer questions like the following:
How tall am I?
Who is the tallest person in our class?
How many people are injured by doors every year?
As you work with decimals in this problem, think about
place value and
how it helps you to sort numbers.
Problem 3.5 Ordering Decimals
A. The table at the right shows the heights of a
class
of sixth-graders.
1. Write Beth and Lana’s heights as fractions.
Who is taller?
2. Order the students according to height from
the shortest to the tallest.
Students’ Heights
| Student | Height (m) |
| Alan | 1.45 |
| Beth | 1.52 |
| Juan | 1.72 |
| Dave | 1.24 |
| Eddie | 1.22 |
| Fred | 1.66 |
| Greg | 1.3 |
| Hiroko | 1.26 |
| Abey | 1.63 |
| Joan | 1.58 |
| Karl | 1.23 |
| Lana | 1.5 |
| Maria | 1.27 |
B. The federal government keeps track of all kinds
of interesting data. The table at the right shows
the number of people injured by various
household items in a recent year per thousand
U.S. residents.
1. Order these items by the number of people
injured from the least to the greatest .
2. Which are more dangerous: beds or
carpets? How do you know?
3. Which item injured about twice as many
people as ladders?
4. Which item injured about 10 times as many
people as televisions?
C. What strategies did you use to order and
Injuries From Household Items
| Item | People Injured (per thousand U.S. residents) |
| Bathtubs and showers | 0.674 |
| Beds | 1.569 |
| Carpets and rugs | 0.404 |
| Ceilings and walls | 0.894 |
| Chairs | 1.008 |
| Doors | 1.143 |
| Ladders | 0.563 |
| Tables | 1.051 |
| Televisions | 0.140 |
| Toilets | 0.195 |
| Windows | 0.446 |
| Prev | Next |