Number and Operations
Section 4: Accurately Solves Problems
NECAP: M(N&O) – X – 4
Vermont: MX: 4
| Definition | Page Number | Definition Number |
| Accurately solves problems | 31 | N&O – 35 |
| Composite number | 35 | N&O – 41 |
| Concept of multiplication | 33 | N&O – 37 |
| Factor | 33 | N&O – 38 |
| Greatest common factor | 35 | N&O – 42 |
| In and out of context | 32 | N&O – 36 |
| Least common multiple | 36 | N&O – 43 |
| Multiples | 34 | N&O – 39 |
| Prime numbers | 35 | N&O – 40 |
| Proportional reasoning | 36 | N&O – 44 |
N&O – 35 Accurately solves problems: The intent of
this GLE is to ensure that students
solve problems at various Depth of Knowledge levels (See NECAP Mathematics Test
Specifications) by performing accurate calculations (without the use of
calculator,
manipulatives, or other tools).
Note: As the Depth of Knowledge levels increase the
computational demand does not necessarily increase.
An attempt is made in the NECAP items to keep the level of computation required
at a reasonable level and
focus on assessing concepts. Also note, two of the three testing sessions of the
NECAP assessment allow
the use of calculators. Items where a calculator would take away from the
construct being measured (e.g.,
accurately solves problems) will appear on the session that does not allow
calculators, manipulatives, or
other tools.
Example 35.1 – (Grade 3) Accurately solves problems
involving … addition and
subtraction of decimals (in the context of money):
|
A gallon of milk costs $3.50. A loaf of bread costs
$1.59. How much does a gallon of milk and a loaf of bread cost together? Show your work. |
Level 1: One-step word problem |
Answer: $5.09; $3.50 + $1.59 = $3.00 + $1.00 + $1.00 + $0.09 = $5.09
Example 35.2 – (Grade 4) Accurately solves problems
involving … addition and
subtraction of decimals :
Use this sign to answer the question below
|
Level 2: Two-step problem |
||||||
|
How much do 6 rides cost? Show your work.
|
Item Source: Lager and Petit, Conserving the Mathematical Construct, 2003. |
Answer: $4.00; $1.50 + $0.50+ $0.50+ $0.50+ $0.50+ $0.50 = $4.00
Example 35.3 – (Grade 6) Accurately solves problems
involving multiple
operations of decimals :
Carolyn and Kim sold 55 cups of lemonade on Monday.
• A cup of lemonade cost $0.10 to make.
• Each cup of lemonade is sold for $0.25.
a. How much did it cost to make 55 cups of lemonade? Show or explain your
work.
b. How much money did Carolyn and Kim collect? Show or explain your work.
c. How much profit did Carolyn and Kim collect for selling 55 cups of lemonade?
Show or explain your work.
|
d. Carolyn and Kim will sell lemonade on Wednesday.
If the cost to make the lemonade and the price remain the same, what is the least number of cups of lemonade Carolyn and Kim need to sell to collect at least $10.00 profit? Show or explain your work. |
Level 3: Solves problem with multiple decision points, and planning |
Item Source: Adapted from
2002 – 6th grade NHIEAP
Answer:
a. $5.50; 55 × $0.10 = $5.50
b. $13.75; Each group of 4 cups sells for $1.00. 55 ÷ 4 =13 remainder 3. So,
selling 55 cups will make
$13.75.
c. $8.25; (55 × $0.25) – (55 × $0.10) = $8.25
d. 67 cups; There are 6 groups of $0.15 in each $1.00 with $0.10 left over. So,
in $10.00 there are 60 groups
of $0.15 with $1.00 left over. Therefore, 66 cups would be $0.10 less than
$10.00 profit. So, they need to sell
67 cups to make at least $10.00 profit.
N&O – 36 In and out of context: In and out of
context means that some problems will
be cast in a context (see Examples 35.1 – 35.3), and others will not be in a
context.
Example 36.1 – Non-contextual example:
What is the least common multiple of 12 and 9?
Answer: 36
N&O – 37 Concept of multiplication: Solving
problems that involve the concept of
multiplication means that the problems must demand an understanding of
multiplication,
not just the application of an algorithm.
Example 37.1:
|
Mrs. Johnson is arranging 30 chairs in rows. What are
all the possible arrangements of the chairs so that: • there are no fewer than 5 chairs in a row, • there are no more than 10 chairs in a row, and • each row has the same number of chairs. |
Level 3: Solves problem with multiple decision points, and planning |
Answer: 3 rows of 10 chairs, 5 rows of 6 chairs, 6 rows of 5 chairs
N&O – 38 Factor: An integer b is a factor of a
given integer if the product of b and some
other integer is the given integer (e.g., given the integer 12, 4 is a factor of
12
since 4·3=12 ). A factor is also called a divisor since it divides the given
integer evenly
(when the given integer is divided by the factor the remainder is 0).
Example 38.1 – Determine whole number factors:
Determine all the whole number factors of 36.
Answer: 1, 2, 3, 4, 6, 9, 12, 18, and 36 are all factors of 36 because each
number divides into 36 a whole
number of times with no remainder.
| Example 38.2 – Determine integer factors: | N&0 – 9 Integer: An integer is a number in the set {…, –3, –2, –1, 0, 1, 2, 3, …}. |
| Determine all the integer factors of 36. |
Answer: The integer factors of are –36, –18, –12, –9, –6,
–4, –3, –2, –1, 1, 2, 3, 4, 6, 9, 12, 18, 36, because
each divides into 36 an integral number of times with no remainder.
At grades K – 6 students will be expected to only generate
the whole number factors for a
given whole number. For 36, students would only have to generate 1, 2, 3, 4, 6,
9, 12, 18,
and 36.
N&O – 39 Multiples: A multiple is a number that is
the product of a given number and
an integer.
Example 39.1: List five multiples of 3.
Sample Answer: 3, 6, 9, 12, and 15 (3 is the given number in this example and
each multiple is produced by
multiplying 3 by 1, 2, 3, 4, and 5, respectively.)
Example 39.2: List all the multiples of 3.
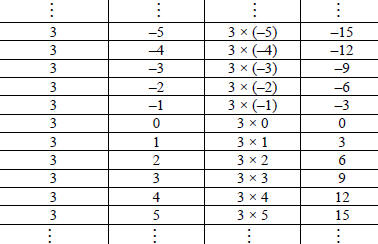
Answer: The set of multiples of 3 is {…, –15, –12, –9, –6, –3, 0, 3, 6, 9, 12,
15, …}.
|
|
|||||||||
N&O – 40 Prime numbers: A prime number is a whole
number greater than 1 that is
only divisible by 1 and itself. (Its only factors are 1 and itself.)
Example 40.1:
5 is a prime number because its only factors are 1 and 5.
11 is a prime number because its only factors are 1 and 11.
12 is NOT a prime number because its factors are 1, 2, 3, 4, 6, and 12.
N&O – 41 Composite number: A composite number is a number that is not
prime (has
factors other than 1 and itself).
Example 41.1:
12 is a composite number since its whole number factors are 1, 2, 3, 4, 6, and
12.
2 is NOT a composite number since its only factors are 1 and itself.
N&O – 42 Greatest Common Factor ( GCF ): The greatest common factor of two
or
more positive integers is the largest factor they have in common.
Example 42.1: What is the greatest common factor (GCF) of 24, 36, and 60?
| Number
|
Factors (Note: Negative factors are not included since we are looking for the greatest common factor.) |
| 24 | 1, 2, 3, 4, 6, 8, 12, 24 |
| 36 | 1, 2, 3, 4, 6, 9, 12, 18, 36 |
| 60 | 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 |
Answer: Though there are many common factors of 24, 36,
and 60, the greatest common factor (GCF) of
24, 36, and 60 is 12.
N&O – 43 Least Common Multiple (LCM): The least
common multiple of two or more
positive integers is the smallest positive multiple that they have in common.
Example 43.1: What is the least common multiple (LCM) of 9, 12, and 18?
| Number | Positive Multiples |
| 9 | 9, 18, 27, 36, 45, 54, 63, 72, 81, … |
| 12 | 12, 24, 36, 48, 60, 72, 84, 96, … |
| 18 | 18, 36, 54, 72, 90, 108, 126, 144, … |
Answer: The least common multiple of 9, 12, and 18 is 36.
N&O – 44 Proportional reasoning: Solving problems involving proportional
reasoning
means to use proportional reasoning in problem solving situations that may
involve
ratios, proportions, rates, slope , scale, similarity, percents, probability, and
others. It is
assumed that throughout instruction students have sufficient opportunities to
connect
each of these situations to proportional reasoning. (e.g., Students should
realize that
proportional relationships are described by linear functions of the form y = kx).
| Prev | Next |